《JavaScript数据结构与算法》读书笔记

发表于 | 分类于 |

这本书让我回顾了一遍大学时候学的数据结构。数据结构和算法是程序员最喜欢也是最痛苦的部分，这本书很轻松的描述了这部分东西，是一本很不错的书。这篇文章记录书中的重点部分，并不会对书中所有的内容都复述一遍，如果希望了解更多的内容可以去看看这本书。由于ES5和ES6思想基本上是相同的，这里只记录ES6的实现。

《JavaScript数据结构与算法》

1. 栈

栈是一种遵从后进先出（LIFO）原则的有序集合。
新添加的或待删除的元素都保存在栈的同一端，称作栈顶，另一端就叫栈底。在栈里，新元素都靠近栈顶，旧元素都接近栈底。

栈的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
let Stack = (function () {

    const items = new WeakMap();

    class Stack {

        constructor () {
            items.set(this, []);
        }

        push(element){
            let s = items.get(this);
            s.push(element);
        }

        pop(){
            let s = items.get(this);
            let r = s.pop();
            return r;
        }

        peek(){
            let s = items.get(this);
            return s[s.length-1];
        }

        isEmpty(){
            return items.get(this).length == 0;
        }

        size(){
            let s = items.get(this);
            return s.length;
        }

        clear(){
            items.set(this, []);
        }

        print(){
            console.log(this.toString());
        }

        toString(){
            return items.get(this).toString();
        }
    }

    return Stack3;
})();

应用：十进制转换成其他进制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function baseConverter(decNumber, base = 2){

    var remStack = new Stack(),
        rem,
        baseString = '',
        digits = '0123456789ABCDEF';

    while (decNumber > 0){
        rem = Math.floor(decNumber % base);
        remStack.push(rem);
        decNumber = Math.floor(decNumber / base);
    }

    while (!remStack.isEmpty()){
        baseString += digits[remStack.pop()];
    }

    return baseString;
}

console.log(baseConverter(100345, 2));// 11000011111111001
console.log(baseConverter(100345, 8));// 303771
console.log(baseConverter(100345, 16));// 187F9

2. 队列

队列是遵循FIFO（First In First Out，先进先出，也称为先来先服务）原则的一组有序的项。
队列在尾部添加新元素，并从顶部移除元素。最新添加的元素必须排在队列的末尾。
队列的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
let Queue = (function () {

    const items = new WeakMap();

    class Queue {

        constructor () {
            items.set(this, []);
        }

        enqueue(element) {
            let q = items.get(this);
            q.push(element);
        }

        dequeue() {
            let q = items.get(this);
            let r = q.shift();
            return r;
        }

        front() {
            let q = items.get(this);
            return q[0];
        }

        isEmpty(){
            return items.get(this).length == 0;
        }

        size(){
            let q = items.get(this);
            return q.length;
        }

        clear(){
            items.set(this, []);
        }

        print(){
            console.log(this.toString());
        }

        toString(){
            return items.get(this).toString();
        }
    }
    return Queue;
})();

优先队列：给定一个优先级，如果新插入的元素按照优先级高低从栈顶到栈尾插入到第一个优先级比他的小元素的前面。
注：这个实现中值越小优先级越高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
let PriorityQueue = (function () {

    class QueueElement {
        constructor(element, priority){
            this.element = element;
            this.priority = priority;
        }
    }

    const items = new WeakMap();

    class PriorityQueue { //extends Queue { //with this approach the private properties are not reachable through inheritance

        constructor () {
            items.set(this, []);
        }

        enqueue(element, priority){
            let queueElement = new QueueElement(element, priority);

            let q = items.get(this);

            let added = false;
            for (let i=0; i<q.length; i++){
                if (queueElement.priority < q[i].priority){// 如果插入的优先级比元素的优先级高
                    q.splice(i,0,queueElement);
                    added = true;
                    break;
                }
            }
            if (!added){//如果前面的优先级都比自己大那么插入到栈尾
                q.push(queueElement);
            }

            items.set(this, q);
        };

        dequeue() {
            let q = items.get(this);
            let r = q.shift();
            items.set(this, q);
            return r;
        }

        front() {
            let q = items.get(this);
            return q[0];
        }

        isEmpty(){
            return items.get(this).length == 0;
        }

        size(){
            let q = items.get(this);
            return q.length;
        }

        clear(){
            items.set(this, []);
        }

        print(){
            let q = items.get(this);
            for (let i=0; i<q.length; i++){
                console.log(`${q[i].element}  - ${q[i].priority}`);
            }
        };
    }
    return PriorityQueue;
})();


let priorityQueue = new PriorityQueue();
priorityQueue.enqueue("John", 2);
priorityQueue.enqueue("Jack", 1);
priorityQueue.enqueue("Ana", 3);
priorityQueue.print();

实战：击鼓传花，使用循环队列来实现。
题目描述：在这个游戏中，孩子们围成一个圆圈，把花尽快地传递给旁边的人。某一时刻传花停止，
这个时候花在谁手里，谁就退出圆圈结束游戏。重复这个过程，直到只剩一个孩子（胜者）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
function hotPotato (nameList, num){

    let queue = new Queue();

    for (let i=0; i<nameList.length; i++){
        queue.enqueue(nameList[i]);
    }

    let eliminated = '';
    while (queue.size() > 1){
        for (let i=0; i<num; i++){
            queue.enqueue(queue.dequeue());
        }
        eliminated = queue.dequeue();
        console.log(eliminated + ' was eliminated from the Hot Potato game.');
    }

    return queue.dequeue();
}

let names = ['John','Jack','Camila','Ingrid','Carl'];
let winner = hotPotato(names, 7);
console.log('The winner is: ' + winner);// The winner is: John

运行示例图：
击鼓传花

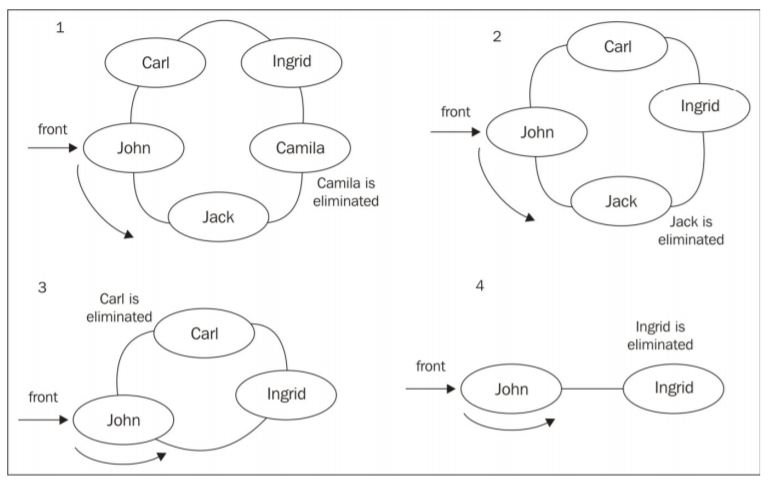
3. 列表
列表是为了解决数组插入或移除消耗内存大而出现的数据结构。
链表存储有序的元素集合，但不同于数组，链表中的元素在内存中并不是连续放置的。每个元素由一个存储元素本身的节点和一个指向下一个元素的引用（也称指针或链接）组成。

列表的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
let LinkedList = (function () {

    class Node {
        constructor(element){
            this.element = element;
            this.next = null;
        }
    }

    const length = new WeakMap();
    const head = new WeakMap();

    class LinkedList {

        constructor () {
            length.set(this, 0);
            head.set(this, null);
        }

        append(element) {

            let node = new Node(element),
                current;

            if (this.getHead() === null) { //first node on list
                head.set(this, node);
            } else {

                current = this.getHead();

                //loop the list until find last item
                while (current.next) {
                    current = current.next;
                }

                //get last item and assign next to added item to make the link
                current.next = node;
            }

            //update size of list
            let l = this.size();
            l++;
            length.set(this, l);
        }

        insert(position, element) {

            //check for out-of-bounds values
            if (position >= 0 && position <= this.size()) {

                let node = new Node(element),
                    current = this.getHead(),
                    previous,
                    index = 0;

                if (position === 0) { //add on first position

                    node.next = current;
                    head.set(this, node);

                } else {
                    while (index++ < position) {
                        previous = current;
                        current = current.next;
                    }
                    node.next = current;
                    previous.next = node;
                }

                //update size of list
                let l = this.size();
                l++;
                length.set(this, l);

                return true;

            } else {
                return false;
            }
        }

        removeAt(position) {

            //check for out-of-bounds values
            if (position > -1 && position < this.size()) {

                let current = this.getHead(),
                    previous,
                    index = 0;

                //removing first item
                if (position === 0) {
                    head.set(this, current.next);
                } else {

                    while (index++ < position) {

                        previous = current;
                        current = current.next;
                    }

                    //link previous with current's next - skip it to remove
                    previous.next = current.next;
                }

                let l = this.size();
                l--;
                length.set(this, l);

                return current.element;

            } else {
                return null;
            }
        }

        remove(element) {

            let index = this.indexOf(element);
            return this.removeAt(index);
        }

        indexOf(element) {

            let current = this.getHead(),
                index = 0;

            while (current) {
                if (element === current.element) {
                    return index;
                }
                index++;
                current = current.next;
            }

            return -1;
        }

        isEmpty() {
            return this.size() === 0;
        }

        size() {
            return length.get(this);
        }

        getHead() {
            return head.get(this);
        }

        toString() {

            let current = this.getHead(),
                string = '';

            while (current) {
                string += current.element + (current.next ? ', ' : '');
                current = current.next;
            }
            return string;

        }

        print() {
            console.log(this.toString());
        }
    }

    return LinkedList;
})();

双向列表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
let DoublyLinkedList = (function () {

    class Node {
        constructor(element) {
            this.element = element;
            this.next = null;
            this.prev = null; //NEW
        }
    }

    const length = new WeakMap();
    const head = new WeakMap();
    const tail = new WeakMap(); //NEW

    class DoublyLinkedList {

        constructor () {
            length.set(this, 0);
            head.set(this, null);
            tail.set(this, null);
        }

        append(element) {

            let node = new Node(element),
                current, _tail;

            if (this.getHead() === null) { //first node on list
                head.set(this, node);
                tail.set(this, node); //NEW
            } else {
                //attach to the tail node //NEW
                _tail = this.getTail();
                _tail.next = node;
                node.prev = _tail;
                tail.set(this, node);
            }

            //update size of list
            let l = this.size();
            l++;
            length.set(this, l);
        }

        insert(position, element) {

            //check for out-of-bounds values
            if (position >= 0 && position <= this.size()) {

                let node = new Node(element),
                    current = this.getHead(),
                    previous,
                    index = 0;

                if (position === 0) { //add on first position

                    if (!this.getHead()) {       //NEW
                        head.set(this, node);
                        tail.set(this, node);
                    } else {
                        node.next = current;
                        current.prev = node; //NEW {1}
                        head.set(this, node);
                    }

                } else if (position === this.size()) { //last item //NEW

                    current = tail;     
                    current.next = node;
                    node.prev = current;
                    tail.set(this, node);

                } else {
                    while (index++ < position) { 
                        previous = current;
                        current = current.next;
                    }
                    node.next = current;
                    previous.next = node;

                    current.prev = node; //NEW
                    node.prev = previous; //NEW
                }

                //update size of list
                let l = this.size();
                l++;
                length.set(this, l);

                return true;

            } else {
                return false;
            }
        }

        removeAt(position) {

            //check for out-of-bounds values
            if (position > -1 && position < this.size()) {

                let _head = this.getHead(),
                    _tail = this.getTail(),
                    current = _head,
                    previous,
                    index = 0;

                //removing first item
                if (position === 0) {

                    _head = current.next; 

                    //if there is only one item, then we update tail as well //NEW
                    if (this.size() === 1) { 
                        _tail = null;
                    } else {
                        _head.prev = null; 
                    }

                } else if (position === this.size() - 1) { //last item //NEW

                    current = _tail; 
                    _tail = current.prev;
                    _tail.next = null;

                } else {

                    while (index++ < position) { 

                        previous = current;
                        current = current.next;
                    }

                    //link previous with current's next - skip it to remove
                    previous.next = current.next; 
                    current.next.prev = previous; //NEW
                }

                head.set(this,_head);
                tail.set(this,_tail);

                //update size of list
                let l = this.size();
                l--;
                length.set(this, l);

                return current.element;

            } else {
                return null;
            }
        }

        remove(element) {

            let index = this.indexOf(element);
            return this.removeAt(index);
        }

        indexOf(element) {

            let current = this.getHead(),
                index = -1;

            //check first item
            if (element == current.element) {
                return 0;
            }

            index++;

            //check in the middle of the list
            while (current.next) {

                if (element == current.element) {
                    return index;
                }

                current = current.next;
                index++;
            }

            //check last item
            if (element == current.element) {
                return index;
            }

            return -1;
        }

        isEmpty() {
            return this.size() === 0;
        }

        size() {
            return length.get(this);
        }

        toString() {

            let current = this.getHead(),
                s = current ? current.element : '';

            while (current && current.next) {
                current = current.next;
                s += ', ' + current.element;
            }

            return s;
        }

        inverseToString() {

            let current = this.getTail(),
                s = current ? current.element : '';

            while (current && current.prev) {
                current = current.prev;
                s += ', ' + current.element;
            }

            return s;
        }

        print() {
            console.log(this.toString());
        }

        printInverse() {
            console.log(this.inverseToString());
        }

        getHead() {
            return head.get(this);
        }

        getTail() {
            return tail.get(this);
        }
    }
    return DoublyLinkedList;
})();

4. 集合
集合是由一组无序且唯一（即不能重复）的项组成的。这个数据结构使用了与有限集合相同的数学概念，但应用在计算机科学的数据结构中。
注：这里的名称叫Set但是最好不要用这个名字，因为ES6中本来就有这个全局变量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
let Set = (function () {

    const items = new WeakMap();

    class Set {

        constructor () {
            items.set(this, {});
        }

        add(value){
            if (!this.has(value)){
                let items_ = items.get(this);
                items_[value] = value;// [键，键]形式
                return true;
            }
            return false;
        }

        delete(value){
            if (this.has(value)){
                let items_ = items.get(this);
                delete items_[value];
                return true;
            }
            return false;
        }

        has(value){
            let items_ = items.get(this);
            return items_.hasOwnProperty(value);
        }

        clear(){
            items.set(this, {});
        }

        size(){
            let items_ = items.get(this);
            return Object.keys(items_).length;
        }


        values(){
            let values = [];
            let items_ = items.get(this);
            for (let i=0, keys=Object.keys(items_); i<keys.length; i++) {
                values.push(items_[keys[i]]);
            }
            return values;
        }

        getItems(){
            return items.get(this);
        }

        //并集 A合B的全部元素
        union(otherSet){
            let unionSet = new Set();

            let values = this.values();
            for (let i=0; i<values.length; i++){
                unionSet.add(values[i]);
            }

            values = otherSet.values();
            for (let i=0; i<values.length; i++){
                unionSet.add(values[i]);
            }

            return unionSet;
        }

        // 交集 A和B公共的部分
        intersection(otherSet){
            let intersectionSet = new Set();

            let values = this.values();
            for (let i=0; i<values.length; i++){
                if (otherSet.has(values[i])){
                    intersectionSet.add(values[i]);
                }
            }

            return intersectionSet;
        }

        // 差集 A去过B的部分
        difference(otherSet){
            let differenceSet = new Set();

            let values = this.values();
            for (let i=0; i<values.length; i++){
                if (!otherSet.has(values[i])){
                    differenceSet.add(values[i]);
                }
            }

            return differenceSet;
        };

        // 子集 B是否包含A
        subset(otherSet){

            if (this.size() > otherSet.size()){
                return false;
            } else {
                let values = this.values();
                for (let i=0; i<values.length; i++){
                    if (!otherSet.has(values[i])){
                        return false;
                    }
                }
                return true;
            }
        };
    }
    return Set;
})();

5. 字典
在字典中，存储的是[键，值]对（其实就是我们的Map），其中键名是用来查询特定元素的。字典和集合很相似，集合以[值，值]的形式存储元素，字典则是以[键，值]的形式来存储元素。字典也称作映射。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
function Dictionary(){

    var items = {};

    this.set = function(key, value){
        items[key] = value; 
    };

    this.delete = function(key){
        if (this.has(key)){
            delete items[key];
            return true;
        }
        return false;
    };

    this.has = function(key){
        return items.hasOwnProperty(key);
        //return value in items;
    };

    this.get = function(key) { 
        return this.has(key) ? items[key] : undefined;
    };

    this.clear = function(){
        items = {};
    };

    this.size = function(){
        return Object.keys(items).length;
    };

    this.keys = function(){
        return Object.keys(items);
    };

    this.values = function(){
        var values = [];
        for (var k in items) {
            if (this.has(k)) {
                values.push(items[k]);
            }
        }
        return values;
    };

    this.each = function(fn) {
        for (var k in items) {
            if (this.has(k)) {
                fn(k, items[k]);
            }
        }
    };

    this.getItems = function(){
        return items;
    }
}

6. 散列表
散列表是散列值（HashCode）和真实值的对应关系，为了避免多个值对应相同HashCode的情况，在存储的时候会存在HashCode所在位置及以后第一个不为空的地方，查找的时候找到hashCode所处的位置，然后从这里开始向后找，知道找到键相同的元素。也可以使用之前开发好的LinkedList和HashCode的对应关系避免。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
function HashTable(){

    var table = [];

    var ValuePair = function(key, value){
        this.key = key;
        this.value = value;

        this.toString = function() {
            return '[' + this.key + ' - ' + this.value + ']';
        }
    };

    var loseloseHashCode = function (key) {
        var hash = 0;
        for (var i = 0; i < key.length; i++) {
            hash += key.charCodeAt(i);
        }
        return hash % 37;
    };

    var djb2HashCode = function (key) {
        var hash = 5381;
        for (var i = 0; i < key.length; i++) {
            hash = hash * 33 + key.charCodeAt(i);
        }
        return hash % 1013;
    };

    var hashCode = function(key){
        return loseloseHashCode(key); // 这里也可以使用djb2HashCode来生成hash值
    };

    this.put = function(key, value){
        var position = hashCode(key);
        console.log(position + ' - ' + key);

        if (table[position] == undefined) {
            table[position] = new ValuePair(key, value);
        } else {
            var index = ++position;
            while (table[index] != undefined){
                index++;
            }
            table[index] = new ValuePair(key, value);
        }
    };

    this.get = function(key) {
        var position = hashCode(key);

        if (table[position] !== undefined){
            if (table[position].key === key) {
                return table[position].value;
            } else {
                var index = ++position;
                while (table[index] === undefined || table[index].key !== key){
                    index++;
                }
                if (table[index].key === key) {
                    return table[index].value;
                }
            }
        }
        return undefined;
    };

    this.remove = function(key){
        var position = hashCode(key);

        if (table[position] !== undefined){
            if (table[position].key === key) {
                table[position] = undefined;
            } else {
                var index = ++position;
                while (table[index] === undefined || table[index].key !== key){
                    index++;
                }
                if (table[index].key === key) {
                    table[index] = undefined;
                }
            }
        }
    };

    this.print = function() {
        for (var i = 0; i < table.length; ++i) {
            if (table[i] !== undefined) {
                console.log(i + ' -> ' + table[i].toString());
            }
        }
    };
}

7. 树
一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点。

树形结构

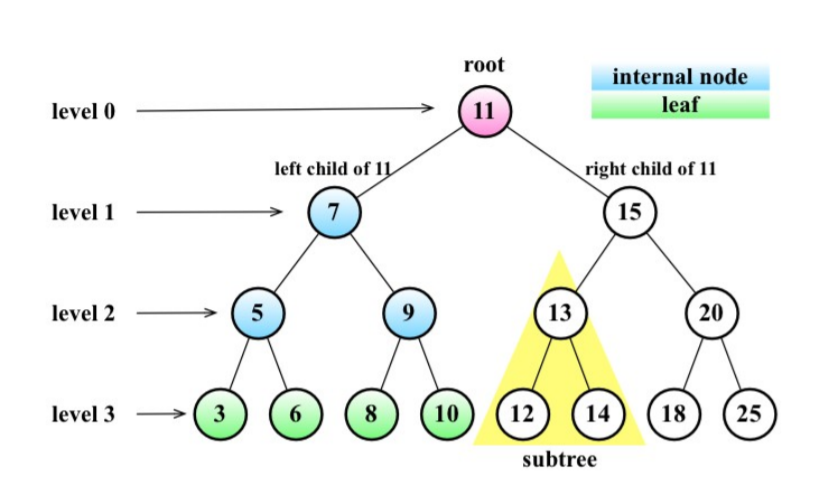
位于树顶部的节点叫作根节点（11）。它没有父节点。树中的每个元素都叫作节点，节点分为内部节点和外部节点。至少有一个子节点的节点称为内部节点（7、5、9、15、13和20是内部节点）。没有子元素的节点称为外部节点或叶节点（3、6、8、10、12、14、18和25是叶节点）。

一个节点可以有祖先和后代。一个节点（除了根节点）的祖先包括父节点、祖父节点、曾祖父节点等。一个节点的后代包括子节点、孙子节点、曾孙节点等。

二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。这些定义有助于我们写出更高效的向/从树中插入、查找和删除节点的算法。二叉树在计算机科学中的应用非常广泛。

二叉搜索树（BST）是二叉树的一种，但是它只允许你在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大（或者等于）的值。

二叉搜索树的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
function BinarySearchTree() {

    var Node = function(key){
        this.key = key;
        this.left = null;
        this.right = null;
    };

    var root = null;

    this.insert = function(key){

        var newNode = new Node(key);

        //special case - first element
        if (root === null){
            root = newNode;
        } else {
            insertNode(root,newNode);
        }
    };

    var insertNode = function(node, newNode){
        if (newNode.key < node.key){
            if (node.left === null){
                node.left = newNode;
            } else {
                insertNode(node.left, newNode);
            }
        } else {
            if (node.right === null){
                node.right = newNode;
            } else {
                insertNode(node.right, newNode);
            }
        }
    };

    this.getRoot = function(){
        return root;
    };

    this.search = function(key){

        return searchNode(root, key);
    };

    var searchNode = function(node, key){

        if (node === null){
            return false;
        }

        if (key < node.key){
            return searchNode(node.left, key);

        } else if (key > node.key){
            return searchNode(node.right, key);

        } else { //element is equal to node.item
            return true;
        }
    };

    //中序遍历 前->中->后
    this.inOrderTraverse = function(callback){
        inOrderTraverseNode(root, callback);
    };

    var inOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            inOrderTraverseNode(node.left, callback);
            callback(node.key);
            inOrderTraverseNode(node.right, callback);
        }
    };

    //前序遍历 中->前->后
    this.preOrderTraverse = function(callback){
        preOrderTraverseNode(root, callback);
    };

    var preOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            callback(node.key);
            preOrderTraverseNode(node.left, callback);
            preOrderTraverseNode(node.right, callback);
        }
    };

    //后序遍历 前->后->中
    this.postOrderTraverse = function(callback){
        postOrderTraverseNode(root, callback);
    };

    var postOrderTraverseNode = function (node, callback) {
        if (node !== null) {
            postOrderTraverseNode(node.left, callback);
            postOrderTraverseNode(node.right, callback);
            callback(node.key);
        }
    };

    // 最小值 最左边的点
    this.min = function() {
        return minNode(root);
    };

    var minNode = function (node) {
        if (node){
            while (node && node.left !== null) {
                node = node.left;
            }

            return node.key;
        }
        return null;
    };

    // 最小值 最右边的点
    this.max = function() {
        return maxNode(root);
    };

    var maxNode = function (node) {
        if (node){
            while (node && node.right !== null) {
                node = node.right;
            }

            return node.key;
        }
        return null;
    };

    this.remove = function(element){
        root = removeNode(root, element);
    };

    var findMinNode = function(node){
        while (node && node.left !== null) {
            node = node.left;
        }

        return node;
    };

    var removeNode = function(node, element){

        if (node === null){
            return null;
        }

        if (element < node.key){
            node.left = removeNode(node.left, element);
            return node;

        } else if (element > node.key){
            node.right = removeNode(node.right, element);
            return node;

        } else { //element is equal to node.item

            //handle 3 special conditions
            //1 - a leaf node
            //2 - a node with only 1 child
            //3 - a node with 2 children

            //case 1
            if (node.left === null && node.right === null){
                node = null;
                return node;
            }

            //case 2
            if (node.left === null){
                node = node.right;
                return node;

            } else if (node.right === null){
                node = node.left;
                return node;
            }

            //case 3
            var aux = findMinNode(node.right);
            node.key = aux.key;
            node.right = removeNode(node.right, aux.key);
            return node;
        }
    };
}

AVL树
BST（二叉搜索树）存在一个问题：取决于你添加的节点数，树的一条边可能会非常深；也就是说，树的一条分支会有很多层，而其他的分支却只有几层。就比如如果第一次添加的是1（根节点），其他节点添加的都是大于1的数，那么其他的节点都会在根节点的右边而左边就没有左子树了。这种情况下添加、移除和搜索某个节点时引起一些性能问题。为了解决这个问题，有一种树叫作Adelson-Velskii-Landi树（AVL树）。AVL树是一种自平衡二叉搜索树，意思是任何一个节点左右两侧子树的高度之差最多为1。也就是说这种树会在添加或移除节点时尽量试着成为一棵完全树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
function AVLTree() {

    var Node = function(key){
        this.key = key;
        this.left = null;
        this.right = null;
    };

    var root = null;

    this.getRoot = function(){
        return root;
    };

    var heightNode = function(node) {
        if (node === null) {
            return -1;
        } else {
            return Math.max(heightNode(node.left), heightNode(node.right)) + 1;
        }
    };

    var rotationLL = function(node) {
        var tmp = node.left;
        node.left = tmp.right;
        tmp.right = node;

        return tmp;
    };

    var rotationRR = function(node) {
        var tmp = node.right;
        node.right = tmp.left;
        tmp.left = node;

        return tmp;
    };

    var rotationLR = function(node) {
        node.left = rotationRR(node.left);
        return rotationLL(node);
    };

    var rotationRL = function(node) {
        node.right = rotationLL(node.right);
        return rotationRR(node);
    };

    var insertNode = function(node, element) {

        if (node === null) {
            node = new Node(element);

        } else if (element < node.key) {

            node.left = insertNode(node.left, element);

            if (node.left !== null) {

                if ((heightNode(node.left) - heightNode(node.right)) > 1){
                    if (element < node.left.key){
                        node = rotationLL(node);
                    } else {
                        node = rotationLR(node);
                    }
                }
            }
        } else if (element > node.key) {

            node.right = insertNode(node.right, element);

            if (node.right !== null) {

                if ((heightNode(node.right) - heightNode(node.left)) > 1){

                    if (element > node.right.key){
                        node = rotationRR(node);
                    } else {
                        node = rotationRL(node);
                    }
                }
            }
        }

        return node;
    };

    this.insert = function(element) {
        root = insertNode(root, element);
    };

    var parentNode;
    var nodeToBeDeleted;

    var removeNode = function(node, element) {
        if (node === null) {
            return null;
        }
        parentNode = node;

        if (element < node.key) {
            node.left = removeNode(node.left, element);
        } else {
            nodeToBeDeleted = node;
            node.right = removeNode(node.right, element);
        }

        if (node === parentNode) { //remove node
            if (nodeToBeDeleted !== null && element === nodeToBeDeleted.key) {
                if (nodeToBeDeleted === parentNode) {
                    node = node.left;
                } else {
                    var tmp = nodeToBeDeleted.key;
                    nodeToBeDeleted.key = parentNode.key;
                    parentNode.key = tmp;
                    node = node.right;
                }
            }
        } else { //do balancing

            if (node.left === undefined) node.left = null;
            if (node.right === undefined) node.right = null;

            if ((heightNode(node.left) - heightNode(node.right)) === 2) {
                if (element < node.left.key) {
                    node = rotationLR(node);
                } else {
                    node = rotationLL(node);
                }
            }

            if ((heightNode(node.right) - heightNode(node.left)) === 2) {
                if (element > node.right.key) {
                    node = rotationRL(node);
                } else {
                    node = rotationRR(node);
                }
            }
        }

        return node;
    };

    this.remove = function(element) {
        parentNode = null;
        nodeToBeDeleted = null;
        root = removeNode(root, element);
    };
}

红黑树的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
function RedBlackTree() {

    var Colors = {
        RED: 0,
        BLACK: 1
    };

    var Node = function (key, color) {
        this.key = key;
        this.left = null;
        this.right = null;
        this.color = color;

        this.flipColor = function(){
            if (this.color === Colors.RED) {
                this.color = Colors.BLACK;
            } else {
                this.color = Colors.RED;
            }
        };
    };

    var root = null;

    this.getRoot = function () {
        return root;
    };

    var isRed = function(node){
        if (!node){
            return false;
        }
        return node.color === Colors.RED;
    };

    var flipColors = function(node){
        node.left.flipColor();
        node.right.flipColor();
    };

    var rotateLeft = function(node){
        var temp = node.right;
        if (temp !== null) {
            node.right = temp.left;
            temp.left = node;
            temp.color = node.color;
            node.color = Colors.RED;
        }
        return temp;
    };

    var rotateRight = function (node) {
        var temp = node.left;
        if (temp !== null) {
            node.left = temp.right;
            temp.right = node;
            temp.color = node.color;
            node.color = Colors.RED;
        }
        return temp;
    };

    var insertNode = function(node, element) {

        if (node === null) {
            return new Node(element, Colors.RED);
        }

        var newRoot = node;

        if (element < node.key) {

            node.left = insertNode(node.left, element);

        } else if (element > node.key) {

            node.right = insertNode(node.right, element);

        } else {
            node.key = element;
        }

        if (isRed(node.right) && !isRed(node.left)) {
            newRoot = rotateLeft(node);
        }

        if (isRed(node.left) && isRed(node.left.left)) {
            newRoot = rotateRight(node);
        }
        if (isRed(node.left) && isRed(node.right)) {
            flipColors(node);
        }

        return newRoot;
    };

    this.insert = function(element) {
        root = insertNode(root, element);
        root.color = Colors.BLACK;
    };
}

8. 图
图是网络结构的抽象模型。图是一组由边连接的节点（或顶点）。学习图是重要的，因为任何二元关系都可以用图来表示。
一个图G = (V, E)由以下元素组成。

V：一组顶点
E：一组边，连接V中的顶点

由一条边连接在一起的顶点称为相邻顶点。
一个顶点的度是其相邻顶点的数量。
如果图中不存在环，则称该图是无环的。如果图中每两个顶点间都存在路径，则该图是连通的。
图可以分为是无向图（边没有方向）和有向图（有向图）。
图也可以是未加权的（目前为止我们看到的图都是未加权的）或是加权的。

图有的三种表示法
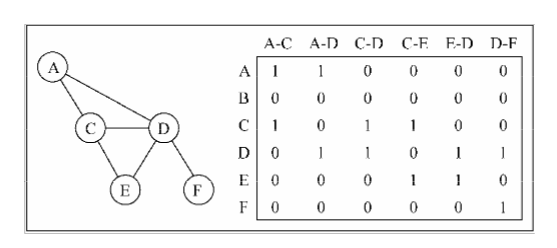
8.1.1 邻接矩阵

邻接矩阵
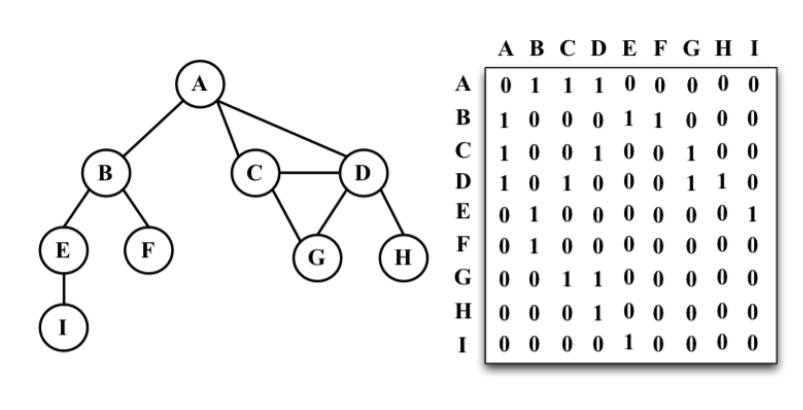
8.1.2 邻接表

邻接表

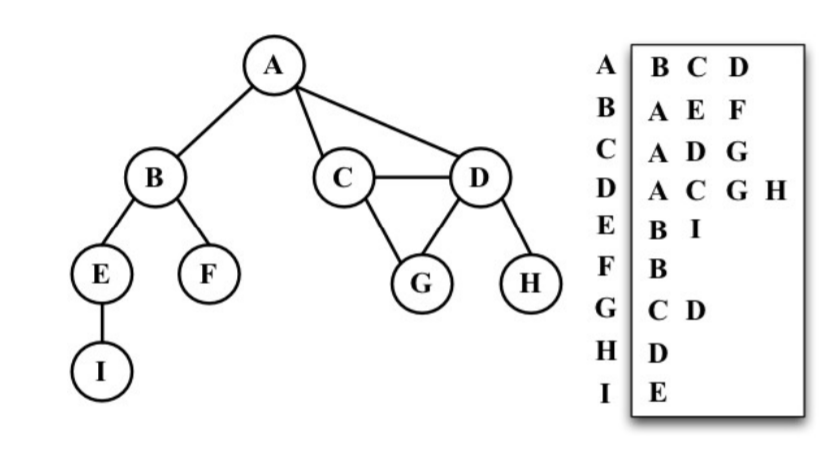
8.1.3 关联矩阵

关联矩阵

图的遍历有两种：
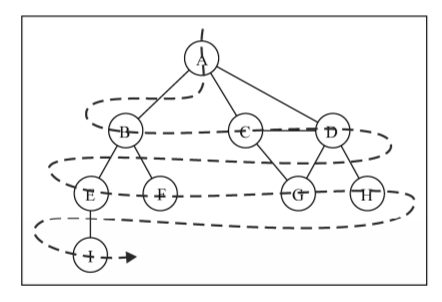
8.2.1 广度优先搜索：

广度优先搜索

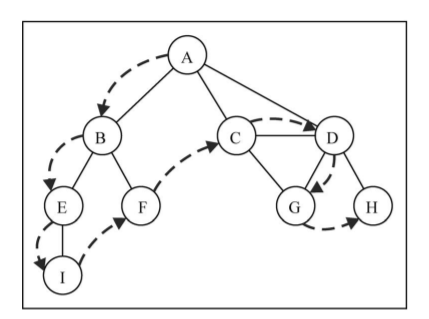
8.2.2 深度优先搜索：

深度优先搜索

图的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
function Graph() {

    var vertices = []; //list

    var adjList = new Dictionary();

    this.addVertex = function(v){
        vertices.push(v);
        adjList.set(v, []); //initialize adjacency list with array as well;
    };

    this.addEdge = function(v, w){
        adjList.get(v).push(w);
        //adjList.get(w).push(v); //commented to run the improved DFS with topological sorting
    };

    this.toString = function(){
        var s = '';
        for (var i=0; i<vertices.length; i++){
            s += vertices[i] + ' -> ';
            var neighbors = adjList.get(vertices[i]);
            for (var j=0; j<neighbors.length; j++){
                s += neighbors[j] + ' ';
            }
            s += '\n';
        }
        return s;
    };

    var initializeColor = function(){
        var color = {};
        for (var i=0; i<vertices.length; i++){
            color[vertices[i]] = 'white';
        }
        return color;
    };

    this.bfs = function(v, callback){

        var color = initializeColor(),
            queue = new Queue();
        queue.enqueue(v);

        while (!queue.isEmpty()){
            var u = queue.dequeue(),
                neighbors = adjList.get(u);
            color[u] = 'grey';
            for (var i=0; i<neighbors.length; i++){
                var w = neighbors[i];
                if (color[w] === 'white'){
                    color[w] = 'grey';
                    queue.enqueue(w);
                }
            }
            color[u] = 'black';
            if (callback) {
                callback(u);
            }
        }
    };

    this.dfs = function(callback){

        var color = initializeColor();

        for (var i=0; i<vertices.length; i++){
            if (color[vertices[i]] === 'white'){
                dfsVisit(vertices[i], color, callback);
            }
        }
    };

    var dfsVisit = function(u, color, callback){

        color[u] = 'grey';
        if (callback) {
            callback(u);
        }
        console.log('Discovered ' + u);
        var neighbors = adjList.get(u);
        for (var i=0; i<neighbors.length; i++){
            var w = neighbors[i];
            if (color[w] === 'white'){
                dfsVisit(w, color, callback);
            }
        }
        color[u] = 'black';
        console.log('explored ' + u);
    };

    // 广度优先搜索（Breadth-First Search，BFS）
    this.BFS = function(v){

        var color = initializeColor(),
            queue = new Queue(),
            d = {},
            pred = {};
        queue.enqueue(v);

        for (var i=0; i<vertices.length; i++){
            d[vertices[i]] = 0;
            pred[vertices[i]] = null;
        }

        while (!queue.isEmpty()){
            var u = queue.dequeue(),
                neighbors = adjList.get(u);
            color[u] = 'grey';
            for (i=0; i<neighbors.length; i++){
                var w = neighbors[i];
                if (color[w] === 'white'){
                    color[w] = 'grey';
                    d[w] = d[u] + 1;
                    pred[w] = u;
                    queue.enqueue(w);
                }
            }
            color[u] = 'black';
        }

        return {
            distances: d,
            predecessors: pred
        };
    };

    //深度优先搜索（Depth-First Search，DFS）
    var time = 0;
    this.DFS = function(){

        var color = initializeColor(),
            d = {},
            f = {},
            p = {};
        time = 0;

        for (var i=0; i<vertices.length; i++){
            f[vertices[i]] = 0;
            d[vertices[i]] = 0;
            p[vertices[i]] = null;
        }

        for (i=0; i<vertices.length; i++){
            if (color[vertices[i]] === 'white'){
                DFSVisit(vertices[i], color, d, f, p);
            }
        }

        return {
            discovery: d,
            finished: f,
            predecessors: p
        };
    };

    var DFSVisit = function(u, color, d, f, p){

        console.log('discovered ' + u);
        color[u] = 'grey';
        d[u] = ++time;
        var neighbors = adjList.get(u);
        for (var i=0; i<neighbors.length; i++){
            var w = neighbors[i];
            if (color[w] === 'white'){
                p[w] = u;
                DFSVisit(w,color, d, f, p);
            }
        }
        color[u] = 'black';
        f[u] = ++time;
        console.log('explored ' + u);
    };
}

9. 排序和查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
function ArrayList(){

    var array = [];

    this.insert = function(item){
        array.push(item);
    };

    var swap = function(array, index1, index2){
        var aux = array[index1];
        array[index1] = array[index2];
        array[index2] = aux;
        //ES2015 swap - Firefox only, for other browser, uncomment code above and coment line below
        //[array[index1], array[index2]] = [array[index2], array[index1]];
    };

    this.toString= function(){
        return array.join();
    };

    this.array= function(){
        return array;
    };

    // 冒泡排序
    this.bubbleSort = function(){
        var length = array.length;

        for (var i=0; i<length; i++){
            console.log('--- ');
            for (var j=0; j<length-1; j++ ){
                console.log('compare ' + array[j] + ' with ' + array[j+1]);
                if (array[j] > array[j+1]){
                    console.log('swap ' + array[j] + ' with ' + array[j+1]);
                    swap(array, j, j+1);
                }
            }
        }
    };

    // 稍微改进一点的冒泡排序 （还可以加标示位来改进）
    this.modifiedBubbleSort = function(){
        var length = array.length;

        for (var i=0; i<length; i++){
            console.log('--- ');
            for (var j=0; j<length-1-i; j++ ){
                console.log('compare ' + array[j] + ' with ' + array[j+1]);
                if (array[j] > array[j+1]){
                    console.log('swap ' + array[j] + ' with ' + array[j+1]);
                    swap(j, j+1);
                }
            }
        }

    };

    // 选择排序：每次寻找数据结构中的最小值放在未排序结构的前面
    this.selectionSort = function(){
        var length = array.length,
            indexMin;

        for (var i=0; i<length-1; i++){
            indexMin = i;
            console.log('index ' + array[i]);
            for (var j=i; j<length; j++){
                if(array[indexMin]>array[j]){
                    console.log('new index min ' + array[j]);
                    indexMin = j;
                }
            }
            if (i !== indexMin){
                console.log('swap ' + array[i] + ' with ' + array[indexMin]);
                swap(i, indexMin);
            }
        }
    };

    // 插入排序：元素插入到已排序的元素中
    this.insertionSort = function(){
        var length = array.length,
            j, temp;
        for (var i=1; i<length; i++){
            j = i;
            temp = array[i];
            console.log('to be inserted ' + temp);
            while (j>0 && array[j-1] > temp){
                console.log('shift ' + array[j-1]);
                array[j] = array[j-1];
                j--;
            }
            console.log('insert ' + temp);
            array[j] = temp;
        }
    };

    var insertionSort_ = function(array){
        var length = array.length,
            j, temp;
        for (var i=1; i<length; i++){
            j = i;
            temp = array[i];
            while (j>0 && array[j-1] > temp){
                array[j] = array[j-1];
                j--;
            }
            array[j] = temp;
        }
    };

    //归并排序
    this.mergeSort = function(){
        array = mergeSortRec(array);
    };

    var mergeSortRec = function(array){

        var length = array.length;

        if(length === 1) {
            console.log(array);
            return array;
        }

        var mid = Math.floor(length / 2),
            left = array.slice(0, mid),
            right = array.slice(mid, length);

        return merge(mergeSortRec(left), mergeSortRec(right));
    };

    var merge = function(left, right){
        var result = [],
            il = 0,
            ir = 0;

        while(il < left.length && ir < right.length) {

            if(left[il] < right[ir]) {
                result.push(left[il++]);
            } else{
                result.push(right[ir++]);
            }
        }

        while (il < left.length){
            result.push(left[il++]);
        }

        while (ir < right.length){
            result.push(right[ir++]);
        }

        console.log(result);

        return result;
    };

    //快速排序
    this.quickSort = function(){
        quick(array,  0, array.length - 1);
    };

    var partition = function(array, left, right) {

        var pivot = array[Math.floor((right + left) / 2)],
            i = left,
            j = right;

        console.log('pivot is ' + pivot + '; left is ' + left + '; right is ' + right);

        while (i <= j) {
            while (array[i] < pivot) {
                i++;
                console.log('i = ' + i);
            }

            while (array[j] > pivot) {
                j--;
                console.log('j = ' + j);
            }

            if (i <= j) {
                console.log('swap ' + array[i] + ' with ' + array[j]);
                swap(array, i, j);
                i++;
                j--;
            }
        }

        return i;
    };

    var quick = function(array, left, right){

        var index;

        if (array.length > 1) {

            index = partition(array, left, right);

            if (left < index - 1) {
                quick(array, left, index - 1);
            }

            if (index < right) {
                quick(array, index, right);
            }
        }
        return array;
    };

    //堆排序
    this.heapSort = function(){
        var heapSize = array.length;

        buildHeap(array);

        while (heapSize > 1) {
            heapSize--;
            console.log('swap (' + + array[0] + ',' + array[heapSize] + ')');
            swap(array, 0, heapSize);
            console.log('heapify ' + array.join());
            heapify(array, heapSize, 0);
        }
    };

    var buildHeap = function(array){
        console.log('building heap');
        var heapSize = array.length;
        for (var i = Math.floor(array.length / 2); i >= 0; i--) {
            heapify(array, heapSize, i);
        }
        console.log('heap created: ' + array.join());
    };

    var heapify = function(array, heapSize, i){
        var left = i * 2 + 1,
            right = i * 2 + 2,
            largest = i;

        if (left < heapSize && array[left] > array[largest]) {
            largest = left;
        }

        if (right < heapSize && array[right] > array[largest]) {
            largest = right;
        }

        console.log('Heapify Index = '+ i + ' and Heap Size = ' + heapSize);

        if (largest !== i) {
            console.log('swap index ' + i + ' with ' + largest + ' (' + + array[i] + ',' + array[largest] + ')');
            swap(array, i, largest);
            console.log('heapify ' + array.join());
            heapify(array, heapSize, largest);
        }
    };

    this.countingSort = function(){

        var i,
            maxValue = this.findMaxValue(),
            sortedIndex = 0,
            counts = new Array(maxValue + 1);

        for (i = 0; i < array.length; i++) {
            if (!counts[array[i]]) {
                counts[array[i]] = 0;
            }
            counts[array[i]]++;
        }

        console.log('Frequencies: ' + counts.join());

        for (i = 0; i < counts.length; i++) {
            while (counts[i] > 0) {
                array[sortedIndex++] = i;
                counts[i]--;
            }
        }
    };

    this.bucketSort = function(bucketSize){

        var i,
            minValue = this.findMinValue(),
            maxValue = this.findMaxValue(),
            BUCKET_SIZE = 5;

        console.log('minValue ' + minValue);
        console.log('maxValue ' + maxValue);

        bucketSize = bucketSize || BUCKET_SIZE;
        var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
        var buckets = new Array(bucketCount);
        console.log('bucketSize = ' + bucketCount);
        for (i = 0; i < buckets.length; i++) {
            buckets[i] = [];
        }

        for (i = 0; i < array.length; i++) {
            buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]);
            console.log('pushing item ' + array[i] + ' to bucket index ' + Math.floor((array[i] - minValue) / bucketSize));
        }

        array = [];
        for (i = 0; i < buckets.length; i++) {
            insertionSort_(buckets[i]);

            console.log('bucket sorted ' + i + ': ' + buckets[i].join());

            for (var j = 0; j < buckets[i].length; j++) {
                array.push(buckets[i][j]);
            }
        }
    };

    this.radixSort = function(radixBase){

        var i,
            minValue = this.findMinValue(),
            maxValue = this.findMaxValue(),
            radixBase = radixBase || 10;

        // Perform counting sort for each significant digit), starting at 1
        var significantDigit = 1;
        while (((maxValue - minValue) / significantDigit) >= 1) {
            console.log('radix sort for digit ' + significantDigit);
            array = countingSortForRadix(array, radixBase, significantDigit, minValue);
            console.log(array.join());
            significantDigit *= radixBase;
        }
    };

    var countingSortForRadix = function(array, radixBase, significantDigit, minValue){
        var i, countsIndex,
            counts = new Array(radixBase),
            aux = new Array(radixBase);

        for (i = 0; i < radixBase; i++) {
            counts[i] = 0;
        }

        for (i = 0; i < array.length; i++) {
            countsIndex = Math.floor(((array[i] - minValue) / significantDigit) % radixBase);
            counts[countsIndex]++;
        }

        for (i = 1; i < radixBase; i++) {
            counts[i] += counts[i - 1];
        }

        for (i = array.length - 1; i >= 0; i--) {
            countsIndex = Math.floor(((array[i] - minValue) / significantDigit) % radixBase);
            aux[--counts[countsIndex]] = array[i];
        }

        for (i = 0; i < array.length; i++) {
            array[i] = aux[i];
        }

        return array;
    };

    // 线性查找
    this.sequentialSearch = function(item){

        for (var i=0; i<array.length; i++){
            if (item === array[i]){
                return i;
            }
        }

        return -1;
    };

    this.findMaxValue = function(){
        var max = array[0];
        for (var i=1; i<array.length; i++){
            if (max < array[i]){
                max = array[i];
            }
        }

        return max;
    };

    this.findMinValue = function(){
        var min = array[0];
        for (var i=1; i<array.length; i++){
            if (min > array[i]){
                min = array[i];
            }
        }

        return min;
    };

    //二分查找
    this.binarySearch = function(item){
        this.quickSort();

        var low = 0,
            high = array.length - 1,
            mid, element;

        while (low <= high){
            mid = Math.floor((low + high) / 2);
            element = array[mid];
            console.log('mid element is ' + element);
            if (element < item) {
                low = mid + 1;
                console.log('low is ' + low);
            } else if (element > item) {
                high = mid - 1;
                console.log('high is ' + high);
            } else {
                console.log('found it');
                return mid;
            }
        }
        return -1;
    };

}

9. 算法模式

递归实现斐波那契函数

1
2
3
4
5
6
function fibonacci(num){
    if (num === 1 || num === 2){
        return 1;
    }
    return fibonacci(num - 1) + fibonacci(num - 2);
}

最少硬币找零问题

动态规划求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function MinCoinChange(coins){
    var coins = coins; 
    var cache = {}; 
    this.makeChange = function(amount) {
        var me = this;
        if (!amount) { 
            return [];
        }
        if (cache[amount]) { 
            return cache[amount];
        }
        var min = [], newMin, newAmount;
        for (var i=0; i<coins.length; i++){ 
            var coin = coins[i];
            newAmount = amount - coin; 
            if (newAmount >= 0){
                newMin = me.makeChange(newAmount); 
            }
            if (newAmount >= 0 && (newMin.length < min.length-1 || !min.length)
                && (newMin.length || !newAmount) {
                min = [coin].concat(newMin); 
                console.log('new Min ' + min + ' for ' + amount); 
            }
        }
        return (cache[amount] = min); 
    };
}

贪心算法求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function MinCoinChange(coins){
    var coins = coins; 
    this.makeChange = function(amount) {
        var change = [],
        total = 0;
        for (var i=coins.length; i>=0; i--){ 
            var coin = coins[i];
            while (total + coin <= amount) { 
                change.push(coin);
                total += coin; 
            }
        }
        return change;
    };
}

使用

1
2
var minCoinChange = new MinCoinChange([1, 5, 10, 25]);
console.log(minCoinChange.makeChange(36));
-------------本文结束 感谢您的阅读-------------
0%