Canvas系列（2）：曲线图形

上一章学的是直线图形的描边和填充，本章我们看看对曲线图形的描边和填充。

圆弧

画弧的API如下

// 圆心：(x,y) 半径：radius 起始弧度：startRadian 结束弧度:endRadian 画弧方向：anticlockwise
context.arc(x, y, radius, startRadian, endRadian, anticlockwise);

// 上述起始弧度和结束弧度都是我们数学上学的弧度就是2 * PI是一圈，
// 通常我们习惯上喜欢用角度作为单位，也就是360°是一圈
// 所以我们更多的使用一下公式
// 起始角度：startAngle 结束角度：endAngle
ccontext.arc(x, y, radius, Math.PI / 180 * startAngle, Math.PI / 180 * endAngle, anticlockwise);

我们先画一个弧线：

context.beginPath();
context.arc(150, 75, 60, Math.PI / 180 * 0, Math.PI / 180 * 90);
context.stroke();

效果如下：

我们的代码是加在上一章最后的坐标系中的，如果直接使用arc画弧的话，那么起始点是上一个绘制的结束，也就是绘制坐标系的结束位置，为了让之前的代码的结束不在作为本次绘制的开始，我们使用了新的APIcontext.beginPath();，用来开启一个新的路径，路径相关的知识会在下一章跟大家分享。我们这里绘制了一个圆心是(150,75)，半径是60，从0度到90度的弧。由上我们可以看出弧的角度是按照我们高中学的坐标系来的。所以，学习是有用的！！！

填充弧线：

context.beginPath();
context.arc(150, 75, 60, Math.PI / 180 * 0, Math.PI / 180 * 90);
context.fill();

效果如下：

描边结果有没有和你预想的不太一样，你脑海中的问题或许下章给你简答的。现在先考虑一下上面最后一个参数anticlockwise，它如果是true的时候表示逆时针绘制，false的时候是顺时针绘制，默认什么都不传相当于传了个undefined，当然也就是false了。我们把这个值设置为true，看看结果，如下：

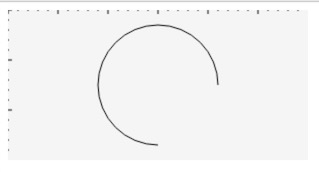
anticlockwise还有一个用处就是制作图形中的图形，可以看一下之前的那篇非零环绕规则。

圆

画圆很简单只要把上面的结束度数改成360就可以了，直接给出结果：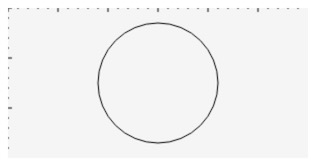

另一种画弧的方法

canvas提供了另一种画弧的方法，就是arcTo:

// (x1, y1) 表示控制点的坐标 （x2, y2）是结束点的坐标 radius是圆弧半径
context.arcTo(x1, y1, x2, y2, radius);

那么你会问起始点的坐标是哪里呢？其实起始点的坐标就是上一次绘制结束时的坐标或者moveTo后的坐标，这个规则跟前面的lineTo是一样的，后面的贝塞尔曲线也跟这是一个道理。arcTo画出来的弧线半径是radius，该弧线与起始点或终点与控制点所在的直线相切。当然看一个例子

context.beginPath();
context.moveTo(210, 75);
context.arcTo(210, 135, 150, 135, 60);
context.stroke();

效果如下：

我把说明也绘制上，如下：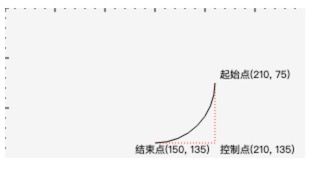

我们上面给的半径是60px，这个半径刚刚好，因为是我本人精心计算的，如果半径不能构成一个很好的弧线那会是什么样子呢？下面分别给出半径是120px和30px的样子：

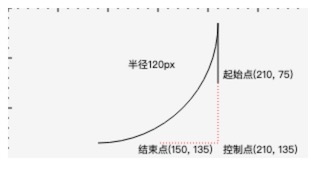
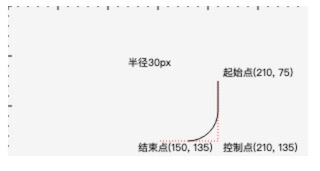
由上可以知道圆弧是一定会过起始点的，有可能会经过终点，起始点有可能是处于切线上。arcTo是没有顺时针画弧还是逆时针画弧的控制参数的，因为起始点控制点和终点就可以决定画弧的方向。

arcTo画弧的应用

arcTo画弧最常见的场景就是画圆角矩形。上节课我们画了一个正方形不知道还有人记得不，不记得的可以会去看看代码，现在我们就把那个矩形加一个半径是20px的圆角。代码如下：

// 之前绘制的是起点在(90, 15)宽和高都是120的矩形
// 所以矩形的右下角是(210, 135)
// 现在加4个20px圆角
context.moveTo(90 +  20, 15);
context.lineTo(210 - 20, 15);
context.arcTo(210, 15, 210, 15 + 20, 20);
context.lineTo(210, 135 - 20);
context.arcTo(210, 135, 210 - 20, 135, 20);
context.lineTo(90 + 20, 135);
context.arcTo(90, 135, 90, 135 - 20, 20);
context.lineTo(90, 15 + 20);
context.arcTo(90, 15, 90 + 20, 15, 20);
context.fillStyle='blue';
context.fill();

效果如下：

二次贝塞尔曲线

我们使用arcTo的时候参数中有一个控制点，一个结束点，还有一个半径。圆弧的圆心到圆弧和起点或终点到控制点的切线的距离刚好是半径。而二次贝塞尔曲线画出的是更好的曲线，它没有半径的限制，画出的弧线并不是某个圆的一部分。它的API如下：

// 其中(cpx, cpy)是控制点 （x, y）是终点
context.quadraticCurveTo(cpx, cpy, x, y);

同样我们画上面的四分之一圆可以这么写，效果与之前是完全一样的：

context.beginPath();
context.moveTo(210, 75);
context.quadraticCurveTo(210, 135, 150, 135);
context.stroke();

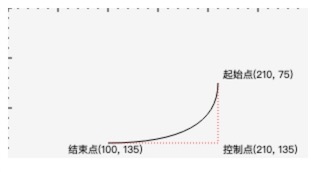
我们稍微修改一下代码：

context.beginPath();
context.moveTo(210, 75);
// 结束点修改了一下
context.quadraticCurveTo(210, 135, 100, 135);
context.stroke();

效果如下：

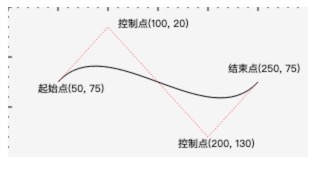
三次贝塞尔曲线

大家猜猜，三次贝塞尔曲线是几个控制点，几个结束点？哈哈，当然是2个控制点，1个结束点了，怎么可能有2个结束的位置呢！API如下：

// 其中(cp1x, cp1y)是控制点1 (cp2x, cp2y)是控制点2 （x, y）是终点
context.bezierCurveTo(cp1x, cp1y, cp2x, cp2y, x, y);

给个例子：

context.beginPath();
context.moveTo(50, 75);
context.bezierCurveTo(100, 20, 200, 130, 250, 75);
context.stroke();

效果图如下：