Canvas系列（14）：实战-小球碰撞

发表于 | 分类于 |

两小球碰撞是Canvas非常经典的案例，他是一个很简单的需求，但做起来却非常复杂。

小球移动操作

根据前面的学习，我们对小球的基本运动了如指掌，直接来一个小球的移动操作，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <meta http-equiv="X-UA-Compatible" content="ie=edge">
  <title>Canvas系列</title>
  <style type="text/css" >
    #canvas{
      background: #eeeeee;
      border: 1px solid #000000;
    }
  </style>
</head>
<body>

  <canvas  id="canvas" width="600" height="400" />

  <script type="text/javascript">
    // 获取元素
    let canvas = document.getElementById('canvas');
    // 获取上下文
    let context = canvas.getContext('2d');

    class Ball {
      constructor(context, options = {}){
        this.context = context;
        this.x = options.x || 0;
        this.y = options.y || 0;
        this.radius = options.radius || 20;
        this.color = options.color || '#000';
        this.vx = options.vx || 0;
        this.vy = options.vy || 0;
        this.ax = options.ax || 0;
        this.ay = options.ay || 0;
      }

      update() {
        this.vx += this.ax;
        this.vy += this.ay;
        this.x += this.vx;
        this.y += this.vy;
      }

      draw() {
        this.context.beginPath();
        this.context.arc(this.x, this.y, this.radius, Math.PI / 180 * 0, Math.PI / 180 * 360);
        this.context.fillStyle = this.color;
        this.context.closePath();
        this.context.fill();
      }
    }

    let balls = []

    balls.push(new Ball(context,{
      x:20,
      y:20,
      vx:3,
      vy:2,
      ay:0.5,
      color:'red',
    }));

    balls.push(new Ball(context,{
      x:canvas.width - 20,
      y:20,
      vx:-3,
      vy:2,
      ay:0.5,
      color:'blue',
    }));


    function checkWalls(ball){
      // 边界反弹
      if (ball.x < ball.radius) {
        ball.x = ball.radius;
        ball.vx *= -1;
      } else if (ball.x > canvas.width - ball.radius) {
        ball.x = canvas.width - ball.radius;
        ball.vx *= -1;
      }

      if (ball.y < ball.radius) {
        ball.y = ball.radius;
        ball.vy *= -1;
      } else if (ball.y > canvas.height - ball.radius) {
        ball.y = canvas.height - ball.radius;
        ball.vy *= -0.95; // 假设能量损耗是0.05
        ball.vx *= 0.99; // 摩擦力
      }
    }

    function draw(ball){
      ball.draw();
    }

    function animate (){
      requestAnimationFrame(animate);
      context.clearRect(0, 0, canvas.width, canvas.height);

      balls.forEach(ball=>{
        // 更新小球的速度
        ball.update();
        // 检测是否碰撞到边界
        checkWalls(ball);
      });

      // 绘制
      balls.forEach(draw);
    }

    animate();
  </script>
</body>
</html>

此时效果如下：

初始效果

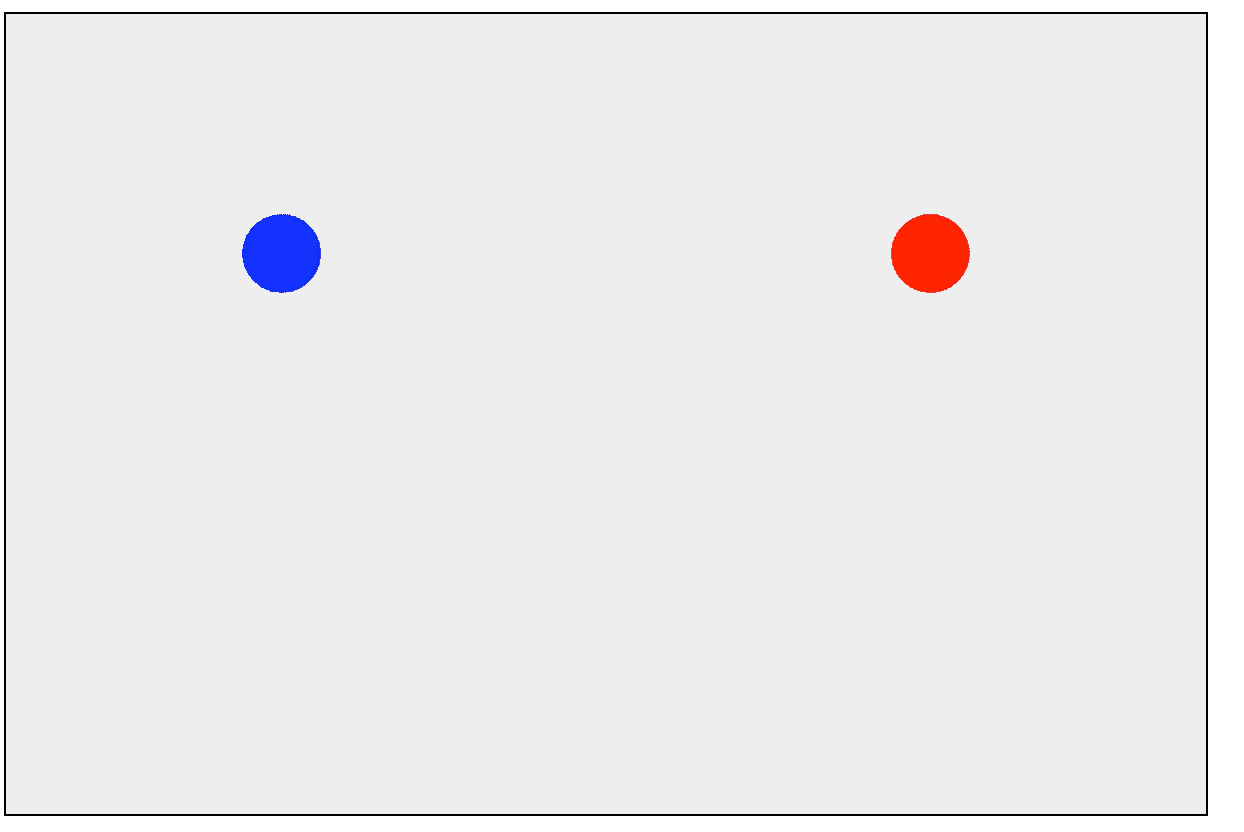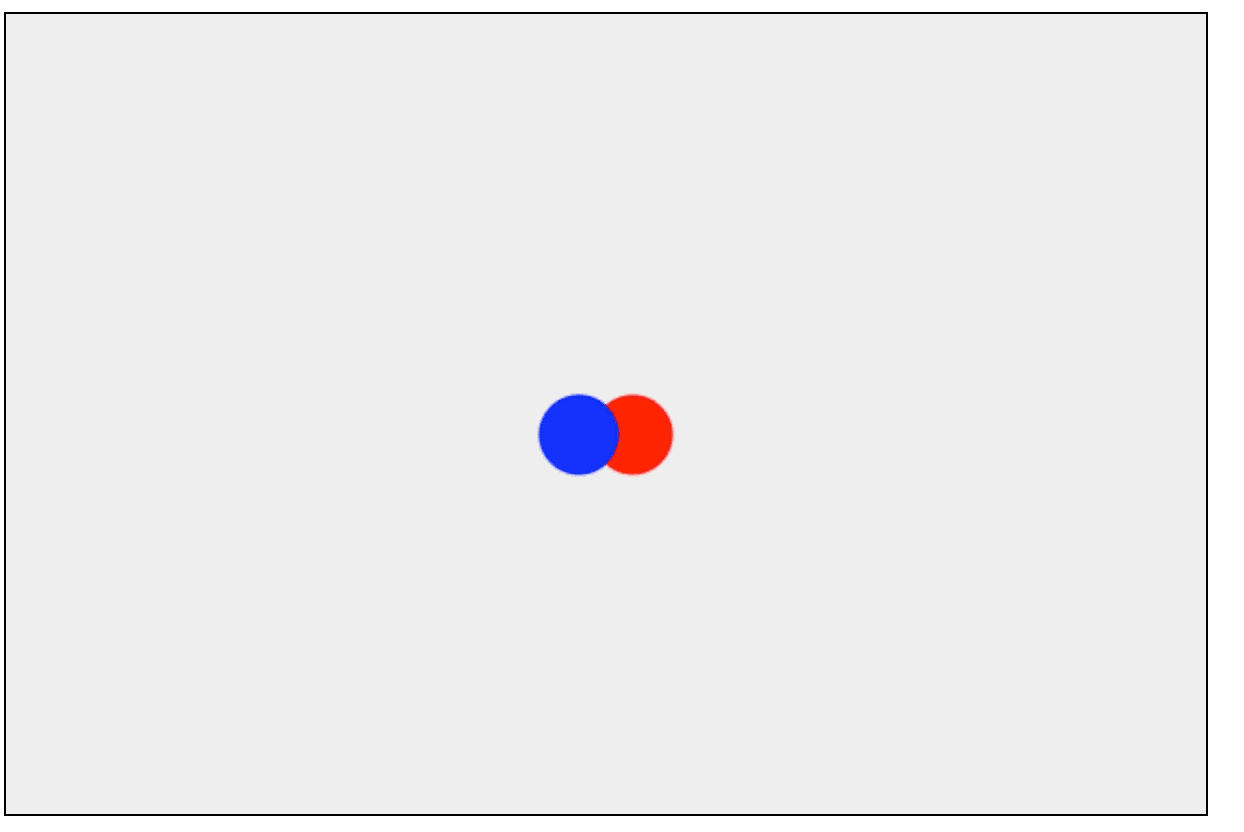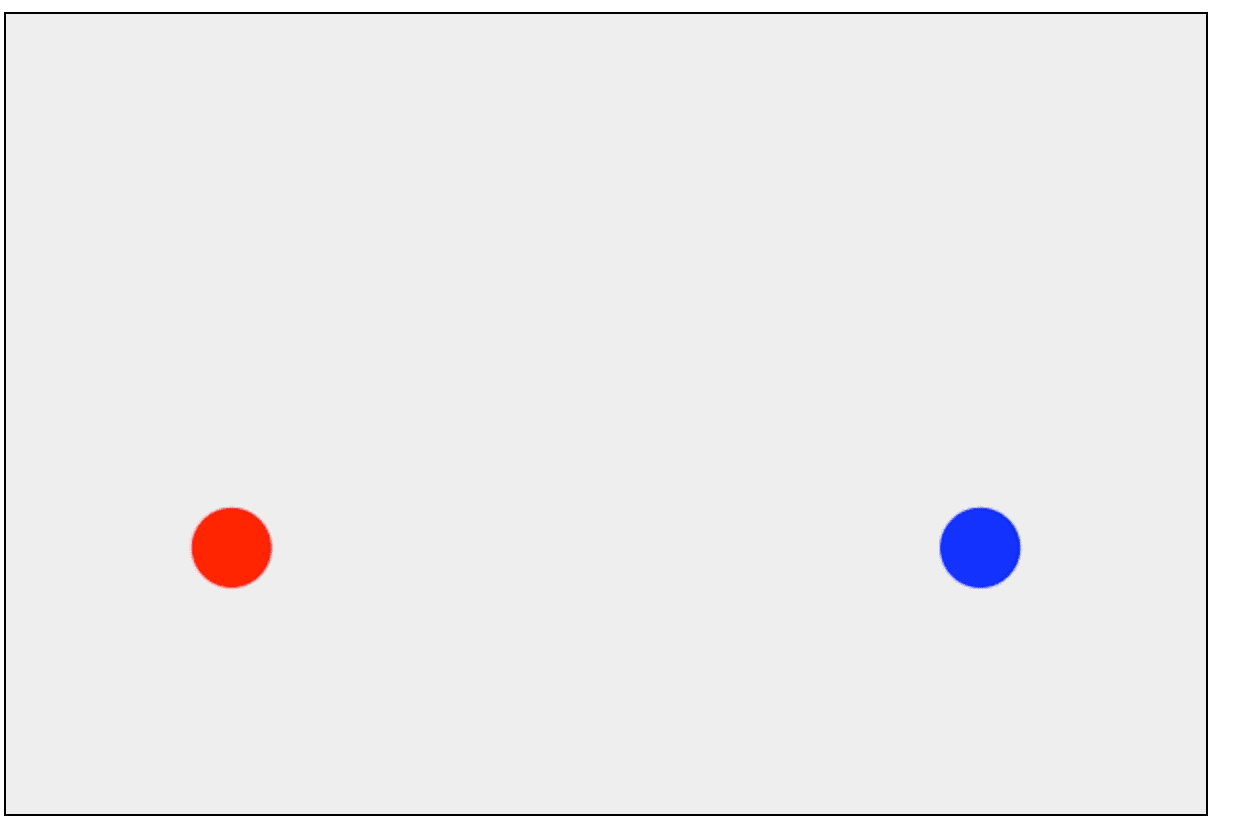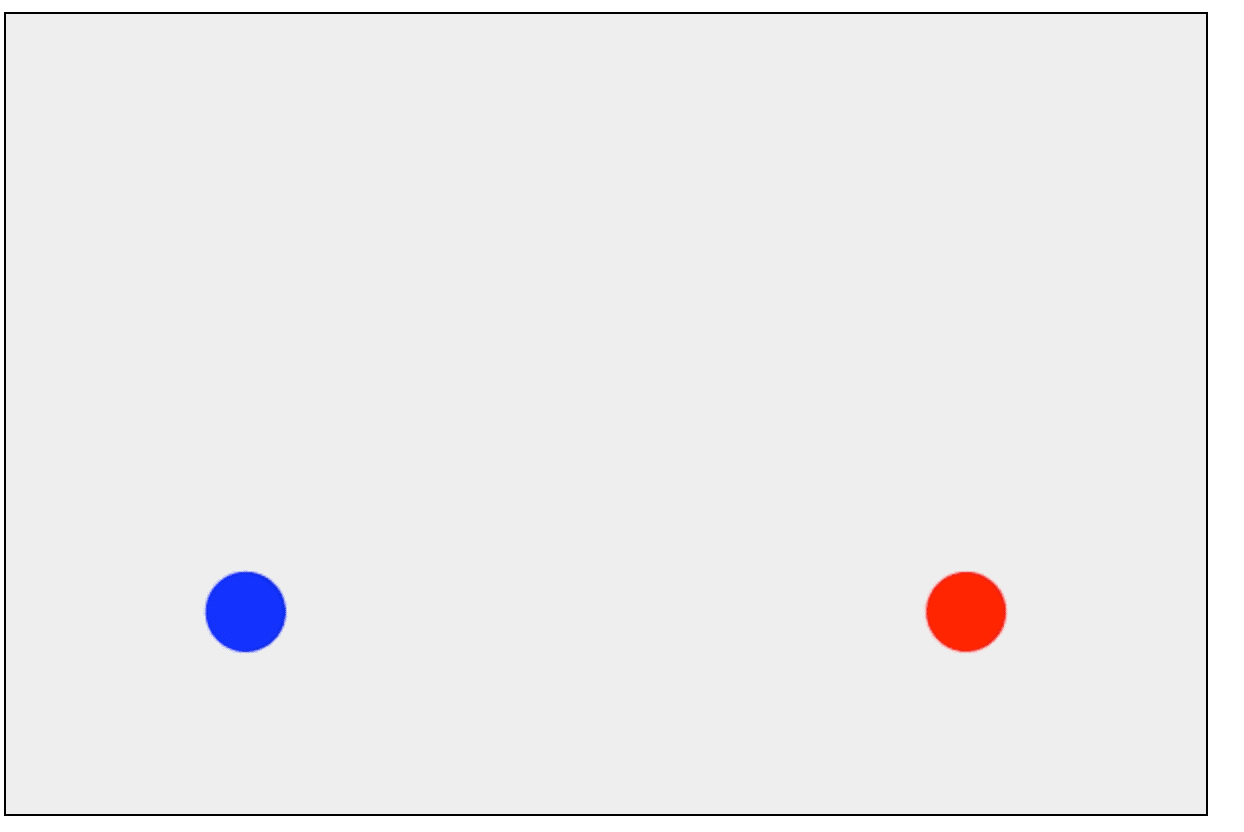
单轴碰撞

上面我们可以看到，小球并没有发生碰撞，今天我们研究的课题就是小球碰撞以后是怎么运动的。为了研究方便，本章节并考虑重力的情况。我们先研究一下只有x轴碰撞的情况，如图：

单轴碰撞

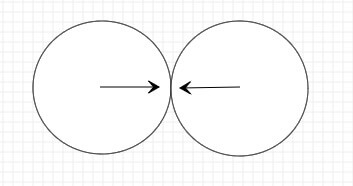
物理理论：

1.小球在碰撞前后，系统总动量是相同的；
2.小球在碰撞前后，系统总动能是相同的。

上面提到了动量和动能，动量等于质量乘以速度，动能等于1/2乘以质量乘以速度的平方。假设第一个小球质量是\(m_0\) ，碰撞前一刹那的瞬时速度是\(v_0\)，碰撞后一刹那的瞬时速度是\(v_{f0}\)；第二个小球质量是\(m_1\)，碰撞前一刹那的瞬时速度是\(v_1\)；碰撞后一刹那的瞬时速度是\(v_{f1}\)，则有公式：

$$
m_0 v_0 + m_1 v_1 = m_0 v_{f0} + m_1 v_{f1} ① \\
\frac{1}{2} m_0 v_0 ^ 2 + \frac{1}{2} m_1 v_1 ^ 2 = \frac{1}{2} m_0 v_{f0} ^ 2 + \frac{1}{2} m_1 v_{f1} ^ 2 ②
$$

上面第一个公式是动量守恒定律，第二个公式是动能守恒定律。求解\(v_{f0}\)和\(v_{f1}\)过程如下：

$$
由 ① 可得：m_0 ( v_0 - v_{f0} ) = m_1 ( v_{f1} - v_1 ) ③ \\
由 ② 可得：m_0 ( v_0 ^ 2 - v_{f0} ^ 2 ) = m_1 ( v_{f1} ^ 2 - v_1 ^ 2 ) ④ \\
④也就是：m_0 ( v_0 - v_{f0} )( v_0 + v_{f0} ) = m_1 ( v_{f1} - v_1 )( v_{f1} + v_1 ) ⑤ \\
由 ③ 和 ⑤ 可得： v_0 + v_{f0} = v_1 + v_{f1} ⑥ \\
⑥也就是：v_{f1} = v_0 + v_{f0} - v_1 ⑦ \\
将 ⑦ 带入 ① 可得：v_{f0} = \frac{ (m_0 - m_1)v_0 + 2 m_1 v_1 }{ m_0 + m_1} \\
同理可得：v_{f1} = \frac{ (m_1 - m_0)v_1 + 2 m_0 v_0 }{ m_0 + m_1} \\
$$

上述解方程过程可以不看，但一定要看最后2行的结论。如果记不住结论也没关系，忘了的时候来这个博客再看看就是了。

这里有一点需要注意一下，上述十字可以看到当两相求的质量相同的时候，碰撞后的速度是碰撞前两速度的交换。

由于本章不考虑重力的情况，现在我们把上个例子中关于重力的部分去掉，然后把小球移动到y轴的中间位置，当两小球碰撞的时，使用上述公式计算新的速度，具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
// 获取元素
let canvas = document.getElementById('canvas');
// 获取上下文
let context = canvas.getContext('2d');

class Ball {
  constructor(context, options = {}){
    this.context = context;
    this.x = options.x || 0;
    this.y = options.y || 0;
    this.radius = options.radius || 20;
    this.color = options.color || '#000';
    this.vx = options.vx || 0;
    this.vy = options.vy || 0;
    this.ax = options.ax || 0;
    this.ay = options.ay || 0;
    this.mass = options.mass || 0; // 质量
    if (this.mass <= 0) {
      this.mass = Math.pow(this.radius, 3) / Math.pow(20, 3);
    }
  }

  update() {
    this.vx += this.ax;
    this.vy += this.ay;
    this.x += this.vx;
    this.y += this.vy;
  }

  draw() {
    this.context.beginPath();
    this.context.arc(this.x, this.y, this.radius, Math.PI / 180 * 0, Math.PI / 180 * 360);
    this.context.fillStyle = this.color;
    this.context.closePath();
    this.context.fill();
  }
}

let balls = []

balls.push(new Ball(context,{
  x:100,
  y:190,
  vx:4,
  // vy:2,
  // ay:0.5,
  color:'red',
}));

balls.push(new Ball(context,{
  x:canvas.width - 100,
  y:190,
  vx:-3,
  // vy:2,
  // ay:0.5,
  color:'blue',
}));


function checkWalls(ball){
  // 边界反弹
  if (ball.x < ball.radius) {
    ball.x = ball.radius;
    ball.vx *= -1;
  } else if (ball.x > canvas.width - ball.radius) {
    ball.x = canvas.width - ball.radius;
    ball.vx *= -1;
  }

  if (ball.y < ball.radius) {
    ball.y = ball.radius;
    ball.vy *= -1;
  } else if (ball.y > canvas.height - ball.radius) {
    ball.y = canvas.height - ball.radius;
    // ball.vy *= -0.95; // 假设能量损耗是0.05
    // ball.vx *= 0.99; // 摩擦力
    ball.vy *= -1;
  }
}

function draw(ball){
  ball.draw();
}

function checkCollision(ball0,ball1) {
  let dist = ball1.x - ball0.x;
  // 检测冲突
  if (Math.abs(dist) < ball0.radius + ball1.radius) {
    // 这里为了保证计算vf1的时候 ball0的vx还是原来的 所以就用变量来定义了 而不是ball0.vx = xxx
    let vf0 = ((ball0.mass - ball1.mass) * ball0.vx + 2 * ball1.mass * ball1.vx) /
      (ball0.mass + ball1.mass);
    let vf1 = ((ball1.mass - ball0.mass) * ball1.vx + 2 * ball0.mass * ball0.vx) /
      (ball0.mass + ball1.mass);

    ball0.vx = vf0;
    ball1.vx = vf1;

    ball0.x += ball0.vx;
    ball1.x += ball1.vx;
  }
}

function animate (){
  requestAnimationFrame(animate);
  context.clearRect(0, 0, canvas.width, canvas.height);

  balls.forEach(ball=>{
    // 更新小球的速度
    ball.update();
    // 检测是否碰撞到边界
    checkWalls(ball);
  });

  for (let i = 0; i < balls.length - 1; i++) {
    for (let j = i + 1; j < balls.length; j++) {
      checkCollision(balls[i], balls[j]);
    }
  }

  // 绘制
  balls.forEach(draw);
}

animate();

此时效果点这里。

上述代码19行，如果没有传进来质量的话就默认是this.mass = Math.pow(this.radius, 3) / Math.pow(20, 3);，因为球体的体积公式和质量公式如下：

$$
V = \frac{4}{3} π R ^ 3 \\
m = ρ V
$$

这里我们令系统的密度\(ρ = \frac{3}{4π * 20 ^ 3}\)，这样就可以保证半径为20像素的小球，其质量是1。

上述方法checkCollision中代码Math.abs(dist) < ball0.radius + ball1.radius用来检测小球是否发生碰撞，如果小球圆心之间的距离小于两个小球的半径之和那么两小球碰撞了，目前因为是单轴的所以就简单的使用距离来判断，后面双轴的时候我们必须使用勾股定理来计算，后面就不再重复了。总的来说上述代码并不难，这里还有一个小技巧，vf1计算的时候我们使用上面的计算速度的公式⑥可以极大的减少运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
function checkCollision(ball0,ball1) {
  let dist = ball1.x - ball0.x;
  // 检测冲突
  if (Math.abs(dist) < ball0.radius + ball1.radius) {
    // 这里为了保证计算vf1的时候 ball0的vx还是原来的 所以就用变量来定义了 而不是ball0.vx = xxx
    let vf0 = ((ball0.mass - ball1.mass) * ball0.vx + 2 * ball1.mass * ball1.vx) /
      (ball0.mass + ball1.mass);
    let vf1 = ((ball1.mass - ball0.mass) * ball1.vx + 2 * ball0.mass * ball0.vx) /
      (ball0.mass + ball1.mass);

    ball0.vx = vf0;
    ball1.vx = vf1;

    ball0.x += ball0.vx;
    ball1.x += ball1.vx;
  }
}

// 修改为：

function checkCollision(ball0,ball1) {
  let dist = ball1.x - ball0.x;
  // 检测冲突
  if (Math.abs(dist) < ball0.radius + ball1.radius) {
    let vxTotal = ball0.vx - ball1.vx;
    ball0.vx = ((ball0.mass - ball1.mass) * ball0.vx + 2 * ball1.mass * ball1.vx) /
      (ball0.mass + ball1.mass);
    ball1.vx = vxTotal + ball0.vx;

    ball0.x += ball0.vx;
    ball1.x += ball1.vx;
  }
}

你会发现效果是一样的，但我们的计算量减小了好多：

单轴碰撞

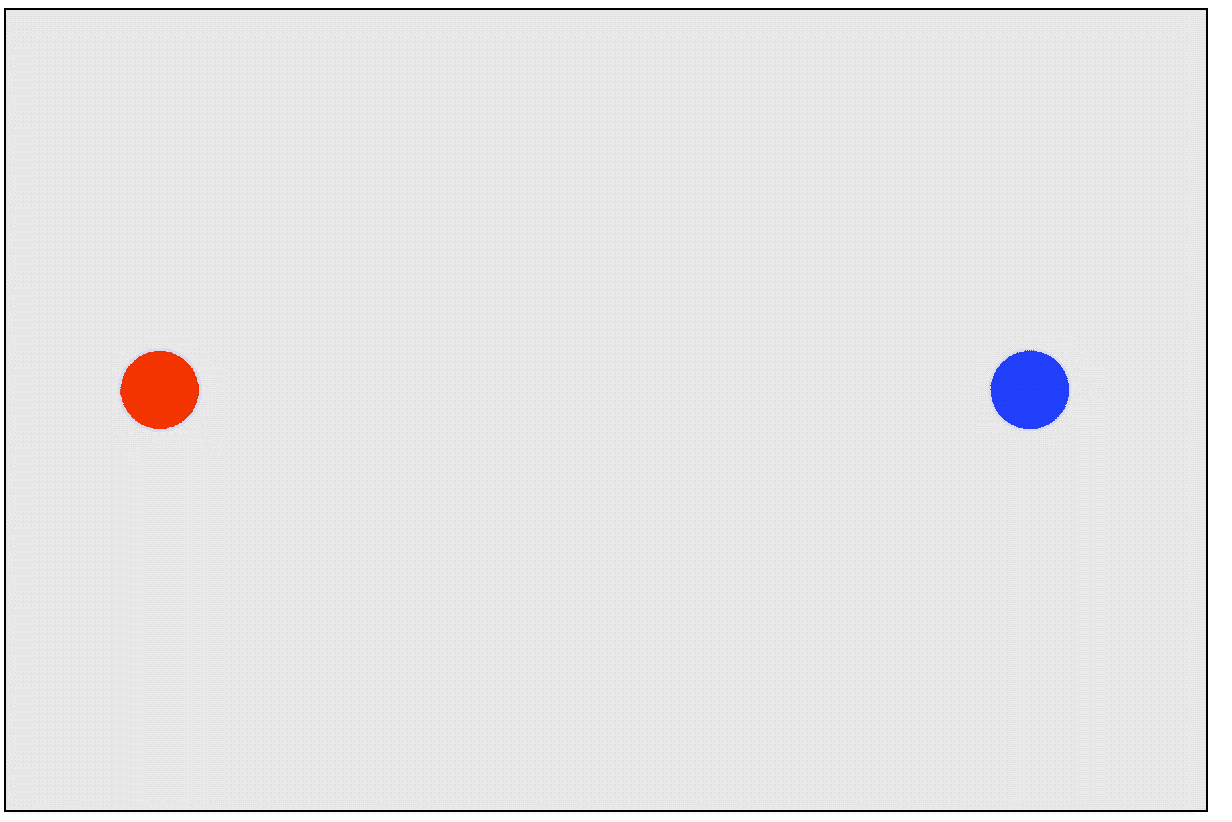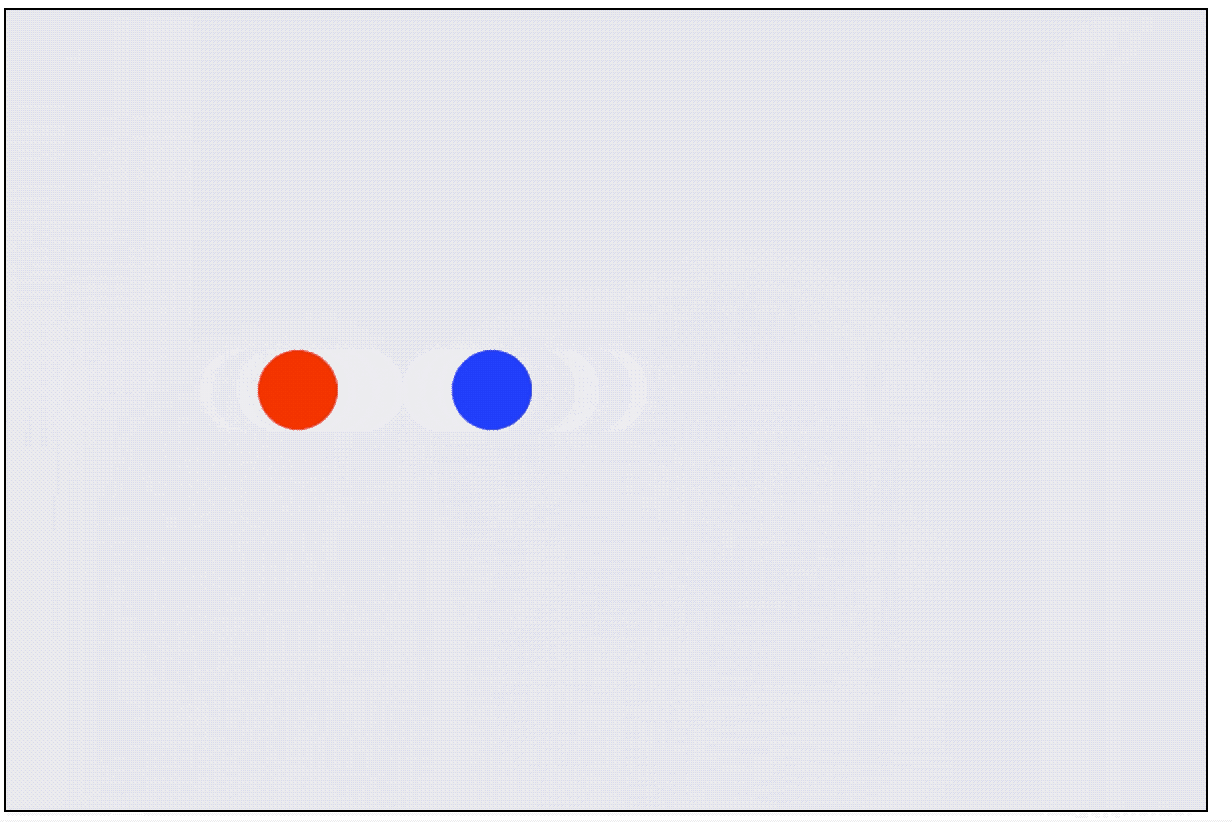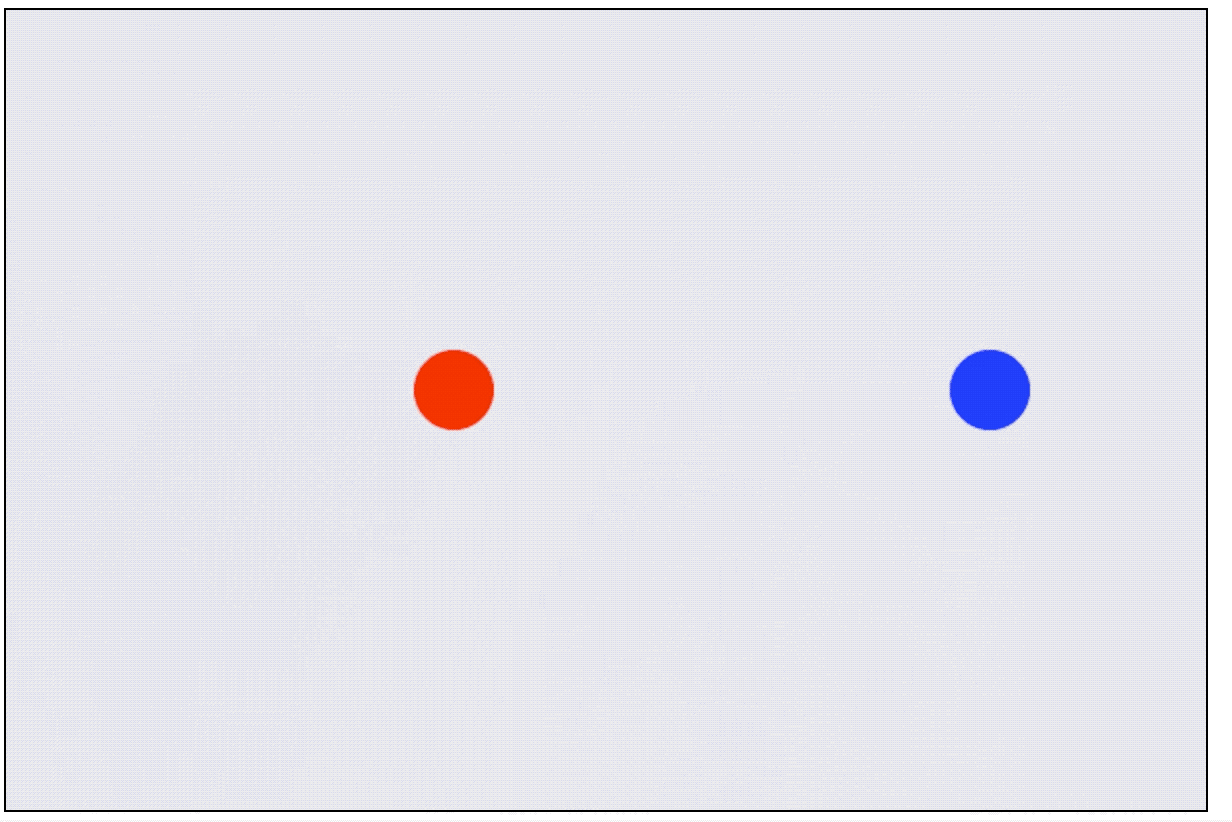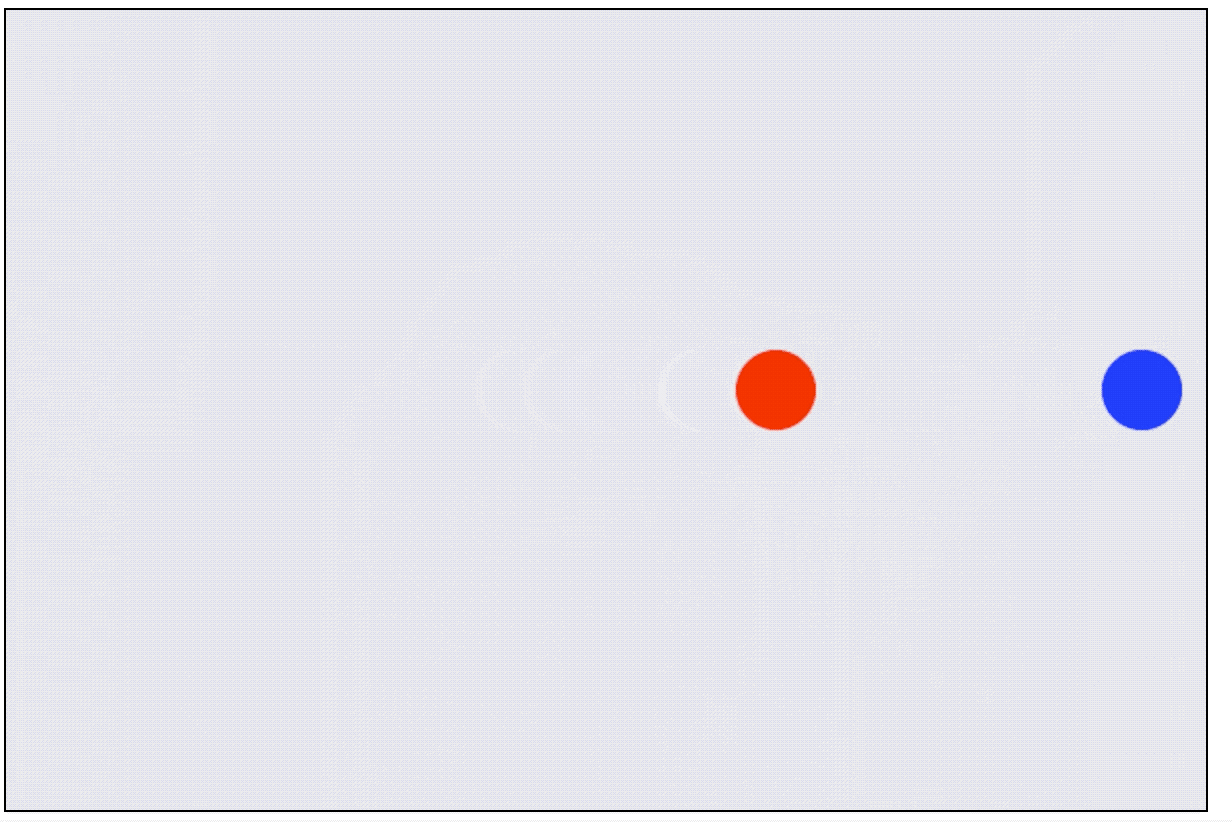
双轴碰撞理论基础

上面单轴碰撞是否已经完全掌握了？一定要多看几遍上面的代码，双轴碰撞比单轴碰撞难多了。大多数情况下，小球的碰撞是没有固定方向的，如图：

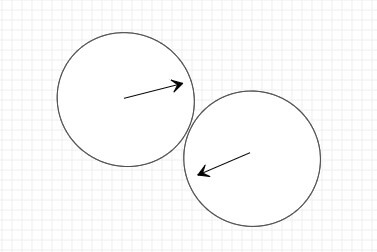
没有固定方向的运动

对于这种情况我们可以把双轴碰撞转换为单轴碰撞。首先旋转坐标系，这里为了方便查看我把圆心之间画了一条红色的线。

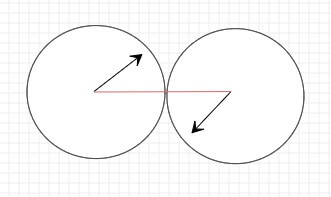
旋转坐标系

这种情况下，就可以把速度分解在旋转后的坐标系上，绿色部分，如图：

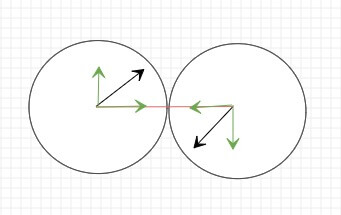
速度的分解

由上，我们在新的坐标系中，水平x轴上相当于是单轴碰撞，而y轴上的速度是垂直于x轴的，对x轴上的速度并不影响。当我们计算出x轴上碰撞后速度后，再跟y轴就可以算出新的合速度，如图所示，其中粉色的是单轴碰撞后计算的速度。

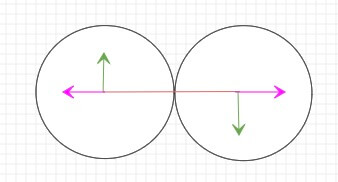
单轴碰撞后的速度

计算合速度（紫色箭头），如下：

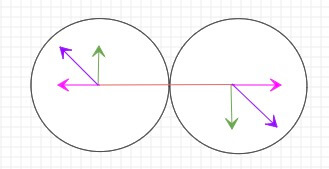
碰撞后的合速度

当然我们上面的坐标系都是旋转后的，现在我们再把坐标系旋转回去，新的紫色箭头就是最终的原始坐标系碰撞后的合速度。

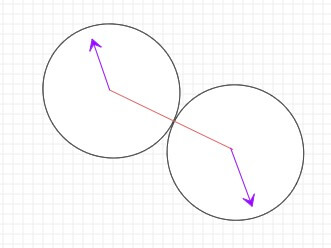
碰撞后的合速度

计算双轴碰撞的整体步骤就是上面这几步，是不是还挺复杂的？主要思路就是把双轴碰撞通过旋跟速度的分解转化为单轴碰撞，然后计算出单轴运动后的速度，再进行运动的合成，算出合速度后再把坐标系旋转回去。

双轴碰撞的代码实现

首先需要计算旋转的角度，只要三行代码，如下：

1
2
3
let dx = ball1.x - ball0.x;
let dy = ball1.y - ball0.y;
let angle = Math.atan2(dy, dx);

这里用到了一个Math.atan2的函数，这个是Canvas中常用的一种计算角度的方法，如图dy与dx使用Math.atan2后的结果就是红色线与x轴的夹角。

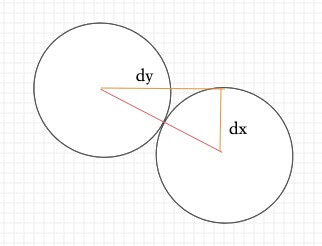
旋转夹角计算

接下来就是计算旋转了，为了方便计算，我们假设左边小球（这里假设左边小球是ball0，右边的是ball1）的圆心坐标是(0,0)，等我们把一切都计算完后，在把各个位置的坐标加上原来小球的圆心位置坐标就可以了。我们先计算以左侧圆心为(0，0)时，旋转后的圆心坐标，如图：

旋转后

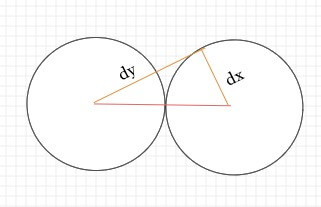
左侧圆就是(0,0)，右侧圆可以根据三角函数来计算：

1
2
3
4
5
6
7
8
let sin = Math.sin(angle);
let cos = Math.cos(angle);
// 左侧小球旋转后小球的位置
let x0 = 0;
let y0 = 0;
// 右侧小球旋转后小球的位置
let x1 = dx * cos + dy * sin;
let y1 = 0;

未旋转前，各小球的速度vx和vy如下图蓝色部分：

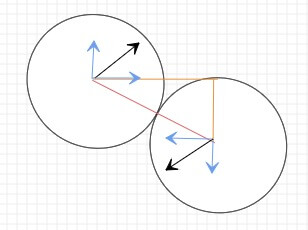
未旋转前的速度分量

旋转以后，为了方便查看我添加了两条垂直于x轴的红线，如图，现在需要通过角度和原来的vx月vy，计算出旋转后的速度分量。

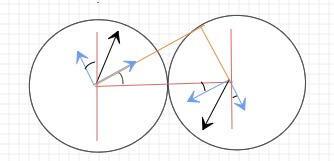
旋转后的速度分量

1
2
3
4
5
6
// 旋转后小球0的速度分量
let vx0 = ball0.vx * cos + ball0.vy * sin;
let vy0 = ball0.vy * cos - ball0.vx * sin;
// 旋转后小球1的速度分量
let vx1 = ball1.vx * cos + ball1.vy * sin;
let vy1 = ball1.vy * cos - ball1.vx * sin;

一定要注意上述代码中符号的问题，我们拿左边的小球（ball0）速度来说，蓝色的两个速度可以分解到新的坐标系中，如下图，紫色的箭头表示分解后的速度，理论上ball0.vx * cos为图中v1的速度，ball0.vy * sin为图中v2的速度，两个速度的合速度的大小是左边速度（v1）的大小减去右边速度（v2）的大小，但是由于Canvas中y轴是向下的，所以图中的情况ball0.vy是朝上的，也就是ball0.vy是一个负数，所以他算出来的右边的速度（v2）也是一个负数，所以两个直接相加就是最终的合速度了。同样的vy的合速度也是一样的。

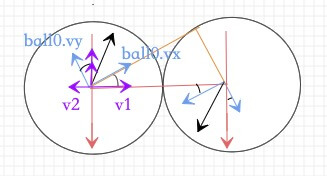
计算公式加减号问题

从上面代码中，我们可以看到计算x轴的分量和y轴的分量其实都是一个模式，这个后面我们可以抽取一个方法。同样的你会发现上面的x1也是遵循这样的公式，y1我们没有计算直接写的0，其实y1也是符合y1 = dy * cos - dx * sin;的，由图我们可以很直观的看到dy * cos和dx * sin是相同的。其实对于Canvas来说，几乎所有的坐标旋转都是这个套路，一定要牢记。

接下来就是激动人心的时刻了，我们需要对旋转后x轴进行单轴碰撞了，代码和上面的单轴碰撞的公式几乎是一致的。

1
2
3
4
5
6
7
let vxTotal = vx0 - vx1;
vx0 = ((ball0.mass - ball1.mass) * vx0 + 2 * ball1.mass * vx1) /
      (ball0.mass + ball1.mass);
vx1 = vxTotal + vx0;
// 两小球的x坐标加上速度 计算出新的x坐标
x0 += vx0;
x1 += vx1;

现在我们碰撞完了，需要对坐标系进行旋转回去，上面旋转了angle角度，旋转回去相当于旋转了-angle，现在是时候展示三角函数的两个等式了：

$$
sin{-\theta} = -sin \theta \\
cos{-\theta} = cos \theta
$$

如果公式忘了，下面这个图会更直观：

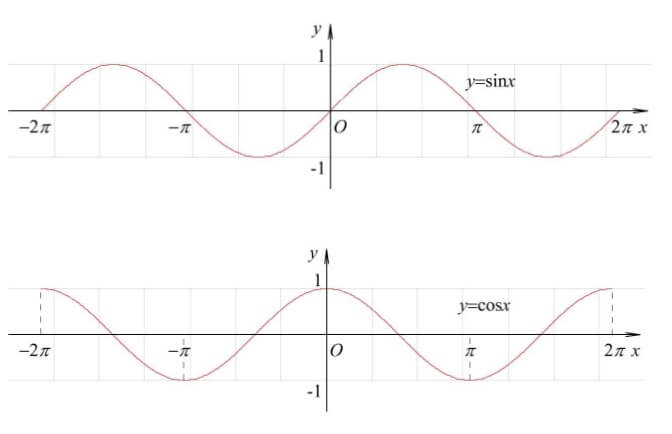
三角函数图像

现在我们只要把负的角度代入上面的函数就好了，所以有如下代码：

1
2
3
4
5
6
7
8
9
10
// 相对于ball0原点为圆心时 旋转回去的坐标
let x0Final = x0 * cos - y0 * sin;
let y0Final = y0 * cos + x0 * sin;
let x1Final = x1 * cos - y1 * sin;
let y1Final = y1 * cos + x1 * sin;
// 相对于 原来的坐标
ball1.x = ball0.x + x1Final;
ball1.y = ball0.y + y1Final;
ball0.x = ball0.x + x0Final;
ball0.y = ball0.y + y0Final;

同样的，我们也需要对速度进行旋转：

1
2
3
4
5
// 速度旋转回去
ball0.vx = vx0 * cos - vy0 * sin;
ball0.vy = vy0 * cos + vx0 * sin;
ball1.vx = vx1 * cos - vy1 * sin;
ball1.vy = vy1 * cos + vx1 * sin;

完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
function checkCollision(ball0,ball1) {
  let dx = ball1.x - ball0.x;
  let dy = ball1.y - ball0.y;
  let dist = Math.sqrt(dx * dx + dy * dy);
  // 检测冲突
  if (dist < ball0.radius + ball1.radius) {
    let angle = Math.atan2(dy, dx);
    let sin = Math.sin(angle);
    let cos = Math.cos(angle);

    // 左侧小球旋转后小球的位置
    let x0 = 0;
    let y0 = 0;
    // 右侧小球旋转后小球的位置
    let x1 = dx * cos + dy * sin;
    let y1 = 0; // 或者 y1 = dy * cos - dx * sin;

    // 旋转后小球0的速度分量
    let vx0 = ball0.vx * cos + ball0.vy * sin;
    let vy0 = ball0.vy * cos - ball0.vx * sin;
    // 旋转后小球1的速度分量
    let vx1 = ball1.vx * cos + ball1.vy * sin;
    let vy1 = ball1.vy * cos - ball1.vx * sin;

    let vxTotal = vx0 - vx1;
    vx0 = ((ball0.mass - ball1.mass) * vx0 + 2 * ball1.mass * vx1) /
          (ball0.mass + ball1.mass);
    vx1 = vxTotal + vx0;
    // 两小球的x坐标加上速度 计算出新的x坐标
    x0 += vx0;
    x1 += vx1;

    // 相对于ball0原点为圆心时 旋转回去的坐标
    let x0Final = x0 * cos - y0 * sin;
    let y0Final = y0 * cos + x0 * sin;
    let x1Final = x1 * cos - y1 * sin;
    let y1Final = y1 * cos + x1 * sin;
    // 相对于 原来的坐标
    ball1.x = ball0.x + x1Final;
    ball1.y = ball0.y + y1Final;
    ball0.x = ball0.x + x0Final;
    ball0.y = ball0.y + y0Final;

    // 速度旋转回去
    ball0.vx = vx0 * cos - vy0 * sin;
    ball0.vy = vy0 * cos + vx0 * sin;
    ball1.vx = vx1 * cos - vy1 * sin;
    ball1.vy = vy1 * cos + vx1 * sin;
  }
}

同时把两小球y方向上的速断放开：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
balls.push(new Ball(context,{
  x:100,
  y:190,
  vx:4,
  vy:2,
  // ay:0.5,
  color:'red',
}));

balls.push(new Ball(context,{
  x:canvas.width - 100,
  y:190,
  vx:-3,
  vy:2,
  // ay:0.5,
  color:'blue',
}));

此时效果如下：

小球碰撞

我们在计算小球旋转的时候有大量相同的代码，现在我们可以抽出一个方法，来优化一下上面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
function rotate (x, y, sin, cos, reverse) {
  return {
    x: (reverse) ? (x * cos + y * sin) : (x * cos - y * sin),
    y: (reverse) ? (y * cos - x * sin) : (y * cos + x * sin)
  };
}


function checkCollision(ball0,ball1) {
  let dx = ball1.x - ball0.x;
  let dy = ball1.y - ball0.y;
  let dist = Math.sqrt(dx * dx + dy * dy);
  // 检测冲突
  if (dist < ball0.radius + ball1.radius) {
    let angle = Math.atan2(dy, dx);
    let sin = Math.sin(angle);
    let cos = Math.cos(angle);

    // boll0旋转后小球的位置
    let pos0 = {x: 0, y: 0};
    // boll1旋转后小球的位置
    let pos1 = rotate(dx, dy, sin, cos, true);
    // ball0旋转后的速度
    let vel0 = rotate(ball0.vx, ball0.vy, sin, cos, true);
    // ball1旋转后的速度
    let vel1 = rotate(ball1.vx, ball1.vy, sin, cos, true);

    let vxTotal = vel0.x - vel1.x;
    vel0.x = ((ball0.mass - ball1.mass) * vel0.x + 2 * ball1.mass * vel1.x) /
              (ball0.mass + ball1.mass);
    vel1.x = vxTotal + vel0.x;

    // 两小球的x坐标加上速度 计算出新的x坐标
    pos0.x += vel0.x;
    pos1.x += vel1.x;
    // 相对于ball0原点为圆心时 旋转回去的坐标
    let pos0F = rotate(pos0.x, pos0.y, sin, cos, false);
    let pos1F = rotate(pos1.x, pos1.y, sin, cos, false);
    // 相对于 原来的坐标
    ball1.x = ball0.x + pos1F.x;
    ball1.y = ball0.y + pos1F.y;
    ball0.x = ball0.x + pos0F.x;
    ball0.y = ball0.y + pos0F.y;
    // 速度旋转回去
    let vel0F = rotate(vel0.x, vel0.y, sin, cos, false);
    let vel1F = rotate(vel1.x, vel1.y, sin, cos, false);
    ball0.vx = vel0F.x;
    ball0.vy = vel0F.y;
    ball1.vx = vel1F.x;
    ball1.vy = vel1F.y;
  }
}

此时效果点击这里

上述代码基本上可以使用了，但是还是有点问题。在多个小球的情况下，当两个小球相撞的时候，上述33行和34行代码中因为加了速度，如果加的速度过大的话，就可以能会导致与其他地方的小球碰撞，为了规避这种问题的产生，碰撞后，碰撞的两个小球的位置刚好移动到没有碰上，也就是两小球刚好相切（外切）。修改上述方法33行和34代码改成下面这个样子：

1
2
3
4
5
6
7
8
9
// 速度的绝对值
var absV = Math.abs(vel0.x) + Math.abs(vel1.x);
// 小球重叠的距离 也就是两个小球最终总共需要移开的距离才能保证两球刚好相切（外切）
// 由于这里只走了一帧 所以这个距离也就是实际的速度之和
let overlap = (ball0.radius + ball1.radius) - Math.abs(pos0.x - pos1.x);
// 速度 除以 absV 就是速度所占的比例 再乘以 overlap 是当前小球这一帧需要走的距离
// 两小球总过走的距离是 overlap
pos0.x += vel0.x / absV * overlap;
pos1.x += vel1.x / absV * overlap;

最后把小球变成多个就可以了：

1
2
3
4
5
6
7
8
9
10
11
12
let balls = [];
let colors = ['red','blue','yellow','green','orange'];
for (let i = 0; i < 10; i++) {
  balls.push(new Ball(context,{
    x: (i + 1) * 50,
    y: 190,
    radius: Math.floor(Math.random() * 10 + 15),
    vx: Math.random() * 6 - 3,
    vy: Math.random() * 6 - 3,
    color: colors[Math.floor(Math.random() * colors.length)],
  }));
}

此时效果如下：

完整效果

完整代码请点击这里。

-------------本文结束 感谢您的阅读-------------
0%