Canvas系列（16）：实战-小球与斜面碰撞

发表于 | 分类于 |

上一章我们讲了小球的拖拽，《小球三部曲》还差一部，今天它来了！本章研究的是小球与斜面碰撞过程。小球与平面或者垂直的面碰撞我们早就会了，在上一章中，有一个函数checkWalls就是检测边界并且处理碰撞，这里的边界就是水平或者垂直的面。现实生活中，大多数情况下，小球碰撞到的并不是平面或者垂直的面，而是斜面，本章就来讨论小球在斜面上运动的过程。

画一个斜面

我们这里简单的画一条线，代表着斜面，Canvas画线很简单只要使用moveTo和lineTo方法就可以了。当然为了代码的可维护性，我们有必要把线封装成一个类，本章的代码是在上一章的代码的基础上添加斜面的操作处理的，画线操作如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Line {
  constructor(context, options = {}) {
    this.context = context;
    this.x1 = options.x1 || 0;
    this.y1 = options.y1 || 0;
    this.x2 = options.x2 || 0;
    this.y2 = options.y2 || 0;
    this.lineWidth = options.lineWidth || 1;
    this.color = options.color || '#000';
    this.rotation = Math.atan2(this.y2 - this.y1, this.x2 - this.x1);
  }

  draw() {
    this.context.save();
    this.context.lineWidth = this.lineWidth;
    this.context.strokeStyle = this.color;
    this.context.beginPath();
    this.context.moveTo(this.x1, this.y1);
    this.context.lineTo(this.x2, this.y2);
    this.context.closePath();
    this.context.stroke();
    this.context.restore();
  }
}

let line = new Line(context,{
  x1: 50, y1: 200,
  x2: 300, y2: 260,
});

// ... 其他代码相同

function animate (){
  // ... 其他代码相同

  // 绘制
  line.draw();
  balls.forEach(draw);
}

上述代码内置了一个rotation字段，用来表示线段与起点所在的x轴的夹角，这个角度后面将会有大用。

小球肯定会穿过斜面，此时的效果（没错就是张静态图片）：

画线

与斜面碰撞的理论基础

之前我们做过小球与小球碰撞，小球碰撞时我们用了非常厉害的一招就是旋转坐标系，把正常的坐标系，转化斜着的坐标系然后来处理，最后再把处理后的坐标系旋转回去。这里也一样，由于水平面的碰撞，我们早就会了，所以我们可以把斜面的碰撞转换为水平面的碰撞。

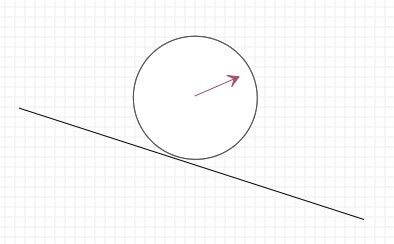
小球与斜面碰撞，初始时候如下图，其中速度可以分解为水平的vx和垂直的vy（图中蓝色部分）。

初始情况

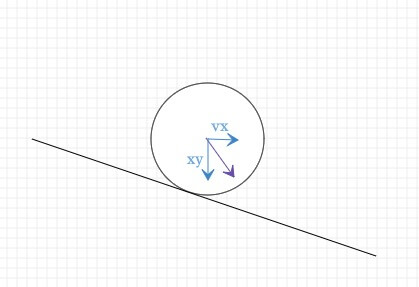
为了方便我们对坐标系进行旋转，转化为水平的位置，此时重新计算新的坐标系的x轴的分速度和y轴的分速度（图中黄色部分），当然还得计算小球在新坐标系中的位置。我们这里把旋转中心设置为斜面最左边的点。

旋转后

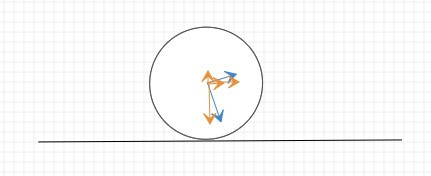
对旋转后的速度做碰撞处理，并求出新的速度。

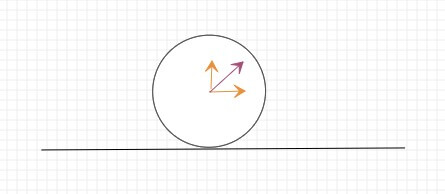
求出新的速度

最后把坐标系旋转回去即可。

旋转回去

小球与斜面碰撞的代码实现

在写代码之初我们修改一下上次代码中的checkWalls方法，把反弹损耗的速度比例用一个变量bounce来定义，这样触碰斜面的时候损耗的速度也用这个变量来计算，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
let bounce = -0.95;

function checkWalls(ball){
  // 边界反弹å
  if (ball.x < ball.radius) {
    ball.x = ball.radius;
    ball.vx *= bounce;
  } else if (ball.x > canvas.width - ball.radius) {
    ball.x = canvas.width - ball.radius;
    ball.vx *= bounce;
  }

  if (ball.y < ball.radius) {
    ball.y = ball.radius;
    ball.vy *= bounce;
  } else if (ball.y > canvas.height - ball.radius) {
    ball.y = canvas.height - ball.radius;
    ball.vy *= bounce; // 假设能量损耗是0.05
    ball.vx *= 0.99; // 摩擦力
  }
}

因为我们要涉及到坐标的旋转，还记得之前小球碰撞时坐标旋转时封装的方法吗？这里选择坐标也得用到这个方法，此外由于sin和cos我们计算时用的多，所以也用一个变量声明一下：

1
2
3
4
5
6
7
8
9
function rotate (x, y, sin, cos, reverse) {
  return {
    x: (reverse) ? (x * cos + y * sin) : (x * cos - y * sin),
    y: (reverse) ? (y * cos - x * sin) : (y * cos + x * sin)
  };
}

let cos = Math.cos(line.rotation);
let sin = Math.sin(line.rotation);

接下来就是前方高能时刻——处理斜面碰撞的过程，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
function animate (){
  requestAnimationFrame(animate);
  context.clearRect(0, 0, canvas.width, canvas.height);

  balls.forEach(ball=>{
    if (selectedBall === ball) {
      trackVelocity();
    } else {
      // 更新小球的速度
      ball.update();

      // 位置以（line.x1，line.y1）为坐标原点来旋转坐标
      let pos = rotate(ball.x - line.x1, ball.y - line.y1, sin, cos, true);
      let vel = rotate(ball.vx, ball.vy, sin, cos, true);
      // 线的y坐标如果小于小球的半径 说明碰撞上了 由于小球在斜线上面所以pos.y是负数 需要加个符号变为正数在比较
      if (-pos.y < ball.radius) {
        // 反弹处理
        vel.y *= bounce;
        pos.y = -ball.radius;
        // 选择回去
        let velF = rotate(vel.x, vel.y, sin, cos, false);
        let posF = rotate(pos.x, pos.y, sin, cos, false);
        ball.vx = velF.x;
        ball.vy = velF.y;
        ball.x = line.x1 + posF.x;
        ball.y = line.y1 + posF.y;
      }

      // 检测是否碰撞到边界
      checkWalls(ball);
    }
  });

  // 绘制
  line.draw();
  balls.forEach(draw);
}

代码和注释，相信你能看得懂，这里需要注意的是小球位置的旋转中心是斜面的最左边，所以位置坐标需要减去左边的坐标，此时的效果如下：

小球与斜面碰撞

由上我们发现我们的代码还是有问题的，目前斜面是无限长的。

只在斜面区域内处理斜面碰撞

如图，只有当小球在粉色区域内才需要判断小球与斜面是否相交，其他情况下都不需要去判断。

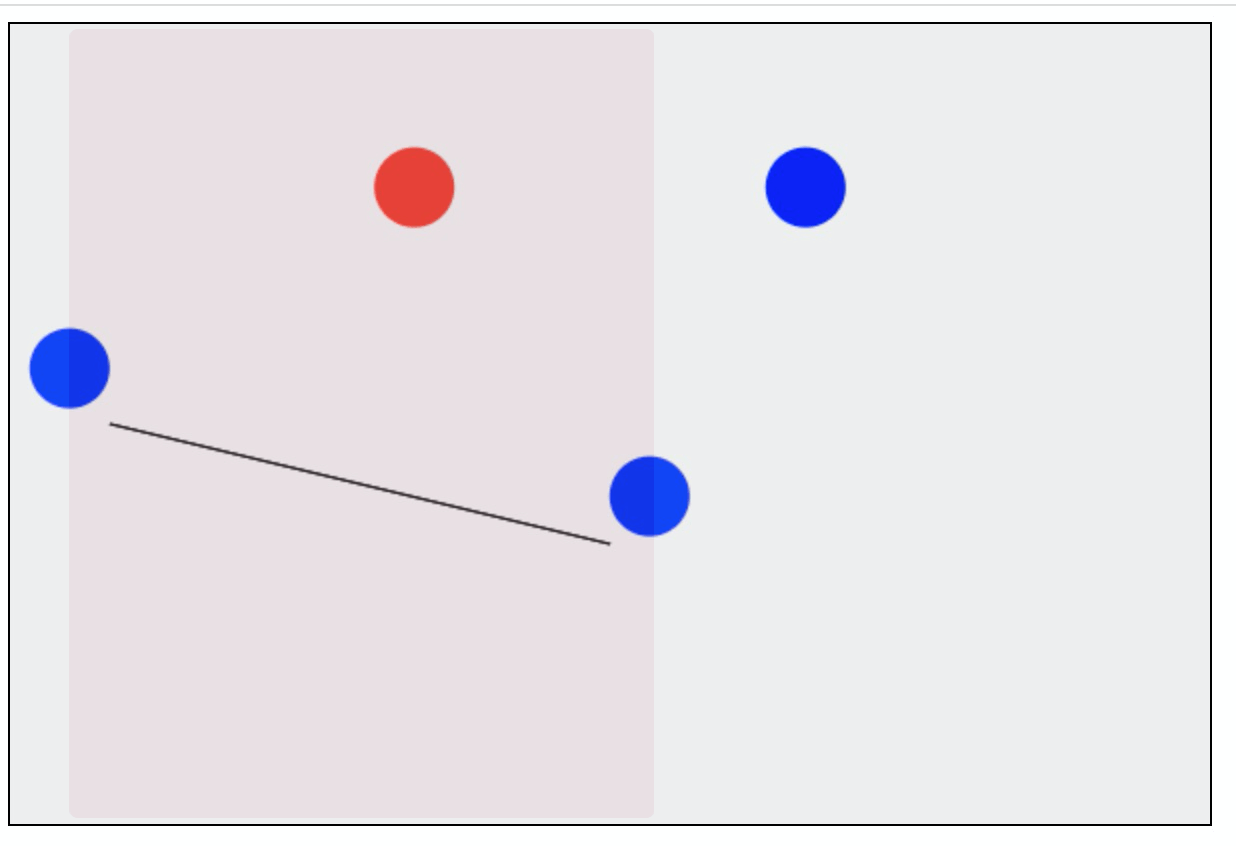
小球与斜面可能碰撞区域

为了方便操作，我们有必要给Line这个类添加一个获取边界的方法getBounds，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Line {
  constructor(context, options = {}) {
    this.context = context;
    this.x1 = options.x1 || 0;
    this.y1 = options.y1 || 0;
    this.x2 = options.x2 || 0;
    this.y2 = options.y2 || 0;
    this.lineWidth = options.lineWidth || 1;
    this.color = options.color || '#000';
    this.rotation = Math.atan2(this.y2 - this.y1, this.x2 - this.x1);
  }

  draw() {
    this.context.save();
    this.context.lineWidth = this.lineWidth;
    this.context.strokeStyle = this.color;
    this.context.beginPath();
    this.context.moveTo(this.x1, this.y1);
    this.context.lineTo(this.x2, this.y2);
    this.context.closePath();
    this.context.stroke();
    this.context.restore();
  }

  getBounds() {
    let minX = Math.min(this.x1, this.x2);
    let minY = Math.min(this.y1, this.y2);
    let maxX = Math.max(this.x1, this.x2);
    let maxY = Math.max(this.y1, this.y2);
    return {
      x: minX,
      y: minY,
      width: maxX - minX,
      height: maxY - minY
    }
  };
}

接下来就很简单了，判断一下是否在粉色的区域就可以了，为了代码更加有条理性，我们把小球与斜面碰撞的过程抽取成一个方法checkLine，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
let bounds = line.getBounds();

function checkLine(ball){
  // 判断小球是否在粉色区域内
  if (ball.x + ball.radius > bounds.x && ball.x - ball.radius < bounds.x + bounds.width){
    // 位置以（line.x1，line.y1）为坐标原点来旋转坐标
    let pos = rotate(ball.x - line.x1, ball.y - line.y1, sin, cos, true);
    let vel = rotate(ball.vx, ball.vy, sin, cos, true);
    // 线的y坐标如果小于小球的半径 说明碰撞上了 由于小球在斜线上面所以pos.y是负数 需要加个符号变为正数在比较
    if (-pos.y < ball.radius) {
      // 反弹处理
      vel.y *= bounce;
      pos.y = -ball.radius;
      // 选择回去
      let velF = rotate(vel.x, vel.y, sin, cos, false);
      let posF = rotate(pos.x, pos.y, sin, cos, false);
      ball.vx = velF.x;
      ball.vy = velF.y;
      ball.x = line.x1 + posF.x;
      ball.y = line.y1 + posF.y;
    }
  }
}

function animate (){
  requestAnimationFrame(animate);
  context.clearRect(0, 0, canvas.width, canvas.height);

  balls.forEach(ball=>{
    if (selectedBall === ball) {
      trackVelocity();
    } else {
      // 更新小球的速度
      ball.update();

      // 检测是否碰撞到斜面
      checkLine(ball);

      // 检测是否碰撞到边界
      checkWalls(ball);
    }
  });

  // 绘制
  line.draw();
  balls.forEach(draw);
}

此时的效果如下：

只有粉色区域内会碰撞

现在我们发现，小球确实是在粉色区域内去弹起，但是如果小球走了斜面的下面，那么小球也会立即弹起，所以我们需要处理一下这个问题。

小球在斜面下的处理

小球在斜面下面的时候也可能会碰撞到斜面，此时也需要反弹，由于我们已经旋转过了，直接添加逻辑就可以了，现在修改checkLine方法，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function checkLine(ball){
    // 判断小球是否在粉色区域内
  if (ball.x + ball.radius > bounds.x && ball.x - ball.radius < bounds.x + bounds.width){
    // 位置以（line.x1，line.y1）为坐标原点来旋转坐标
    let pos = rotate(ball.x - line.x1, ball.y - line.y1, sin, cos, true);
    let vel = rotate(ball.vx, ball.vy, sin, cos, true);
    // 当小球中心距离斜面的距离小于半径的时说明已经相碰撞了
    if (Math.abs(pos.y) < ball.radius) {
      // 判断小球是上面碰撞还是下面碰撞
      if (pos.y - vel.y <= 0) {
        pos.y = -ball.radius;
      } else {
        pos.y = ball.radius;
      }
      vel.y *= bounce;
      // 选择回去
      let velF = rotate(vel.x, vel.y, sin, cos, false);
      let posF = rotate(pos.x, pos.y, sin, cos, false);
      ball.vx = velF.x;
      ball.vy = velF.y;
      ball.x = line.x1 + posF.x;
      ball.y = line.y1 + posF.y;
    }
  }
}

判断小球是上面碰撞还是下面碰撞的时候我们用到了pos.y - vel.y <= 0来判断是上面，一般情况下只要判断pos.y <= 0就可以说明小球在斜面的上面，毕竟旋转后的y坐标小于斜面的y坐标基本上可以说是在上面了。但是因为本次绘制的时候我们拿到的位置是已经加上y坐标上的速度了，当前帧的位置可能会让代码出现bug，就比如小球是从上往下撞到斜面（此时已经按平面处理了）的，由于本次加了一个速度，就有一定的可能让pos.y大于0，也就是小球加了个速度可能会使位置到了斜面的下方；为了规避这种情况，我们使用没有加y轴上速度时候的y轴的值，也就是上一帧y轴的距离，即pos.y - vel.y来判断。

我们的斜面碰撞终于写完了，当然现在先别高兴的太早了，上一章拖拽的时候小球被甩出时很可能会去一个很大的速度，这样就会有“穿墙”的可能性，为了避免这种问题的发生我们让甩出去的合速度最大为半径的大小，修改方法trackVelocity，如下：

1
2
3
4
5
6
7
8
9
10
11
12
function trackVelocity () {
  selectedBall.vx = selectedBall.x - oldX;
  selectedBall.vy = selectedBall.y - oldY;
  let v = Math.hypot(selectedBall.vx, selectedBall.vy);
  if (v > selectedBall.radius) {
    let rate = selectedBall.radius / v;
    selectedBall.vx *= rate;
    selectedBall.vy *= rate;
  }
  oldX = selectedBall.x;
  oldY = selectedBall.y;
}

大功告成，完整代码请点这里。

此时的效果如下：

完整效果

-------------本文结束 感谢您的阅读-------------
0%